题目内容
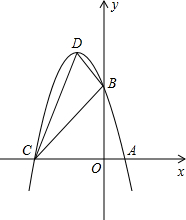 已知抛物线y=-x2+bx+c的图象经过点A(1,0)和B(0,5).
已知抛物线y=-x2+bx+c的图象经过点A(1,0)和B(0,5).(1)求这个抛物线的解析式.
(2)设(1)中抛物线与x轴的另一交点为C.抛物线的顶点为D,是求出点C、D的坐标和△BCD的面积.
(3)点P是线段OC上一点,过点P作PH⊥x轴,与抛物线交于H点.是否存在点P,使得线段BC把△PCH分成面积相等的两部分?若存在,请求出点P的坐标.若不存在,请说明理由.
分析:(1)将点A、B的坐标代入可得出b、c的值,继而得出这个抛物线的解析式;
(2)由抛物线解析式可求出点C、点D的坐标,过顶点D作DE⊥x轴交线段BC于E点,求出点E坐标,然后根据S△BCD=S△BDE+S△DEC,即可得出答案.
(3)若BC分△PCH为面积相等两部分,则需PH与线段BC的交点是线段PH的中点,设点P(x,0),则Q(x,x+5),H(x,-x2-4x+5),根据HQ=QP,可得关于x的方程,解出即可.
(2)由抛物线解析式可求出点C、点D的坐标,过顶点D作DE⊥x轴交线段BC于E点,求出点E坐标,然后根据S△BCD=S△BDE+S△DEC,即可得出答案.
(3)若BC分△PCH为面积相等两部分,则需PH与线段BC的交点是线段PH的中点,设点P(x,0),则Q(x,x+5),H(x,-x2-4x+5),根据HQ=QP,可得关于x的方程,解出即可.
解答:解:(1)把(1,0)(0,5)代入y=-x2+bx+c得:
,
解得:
,
故二次函数解析式为y=-x2-4x+5.
(2)令y=0,则0=-x2-4x+5,
解得:x1=1,x2=-5,
∴C(-5,0),
由y=-x2-4x+5=-(x+2)2+9得顶点D(-2,9),
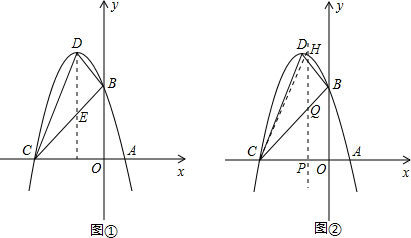
过顶点D作DE⊥x轴交线段BC于E点如图①,
由点B、C得直线BC解析式为y=x+5,
∴当x=-2时,y=3,
∴E(-2,3),
∴DE=6,
∴S△BCD=S△BDE+S△CDE=
×5×6=15.
(3)存在.
理由如下:
若BC分△PCH为面积相等两部分,则需PH与线段BC的交点是线段PH的中点,
若设PH与线段BC的交点为Q,如图②,
设点P(x,0),则Q(x,x+5),H(x,-x2-4x+5),
由HQ=QP得,-x2-4x+5-(x+5)=x+5,
解得:x1=-1,x2=-5(舍去),
∴存在这样的点P,其坐标为P(-1,0).
|
解得:
|
故二次函数解析式为y=-x2-4x+5.
(2)令y=0,则0=-x2-4x+5,
解得:x1=1,x2=-5,
∴C(-5,0),
由y=-x2-4x+5=-(x+2)2+9得顶点D(-2,9),
过顶点D作DE⊥x轴交线段BC于E点如图①,
由点B、C得直线BC解析式为y=x+5,
∴当x=-2时,y=3,
∴E(-2,3),
∴DE=6,
∴S△BCD=S△BDE+S△CDE=
| 1 |
| 2 |

(3)存在.
理由如下:
若BC分△PCH为面积相等两部分,则需PH与线段BC的交点是线段PH的中点,
若设PH与线段BC的交点为Q,如图②,
设点P(x,0),则Q(x,x+5),H(x,-x2-4x+5),
由HQ=QP得,-x2-4x+5-(x+5)=x+5,
解得:x1=-1,x2=-5(舍去),
∴存在这样的点P,其坐标为P(-1,0).
点评:本题考查二次函数的综合题,涉及了待定系数法求函数解析式、三角形的面积,每一小问的解法可能不止一种,同学们可以自己探索,例如:本题第二小问,可以求出四边形DCOB的面积,然后减去△OBC的面积求△BCD的面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知抛物线y=x2-8x+c的顶点在x轴上,则c等于( )
| A、4 | B、8 | C、-4 | D、16 |
 (1)求b+c的值;
(1)求b+c的值; (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.