Question

（2013•荔湾区一模）方程x²+1=

2

x

的正根的个数为（　　）

A．3个

B．2个

C．1个

D．0个

Answer 1

分析：方程x²+1=

2

x

的正根个数问题先转化为函数图象的交点问题，用数形结合法，画出图象由图可得正根个数．

解答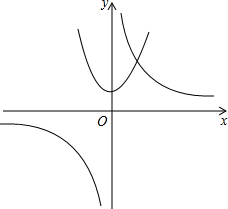：解：方程x²+1=

2

x

的正根个数问题先转化为函数图象的交点问题，
画出左右两边式子的式子，分别画出函数y=x²+1，y=

2

x

图象．
由图可得，正根个数为1．
故选：C．

点评：此题主要考查了二次函数图象与反比例函数图象，本题学生很容易去分母得x³+x=2，然后解方程，不易实现目标．事实上，只要利用数形结合的思想，观察图象在第一象限只有1个交点．