题目内容
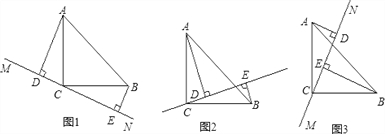
【题目】在△ABC中,∠ACB=90AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当MN绕点C旋转到图1的位置时,请你探究线段DE、AD、BE之间的数量关系(直接写出结论,不要求写出证明过程);
(2)当MN绕点C旋转到图2的位置时,你在(1)中得到的结论是否发生变化?请写出你的猜想,并加以证明;
(3)当MN绕点C旋转到图3的位置时,你在(1)中得到的结论是否发生变化?请写出你的猜想,并加以证明。
【答案】见解析
【解析】【试题分析】
(1)思路先证明△ACD≌△CBE.(AAS)再利用全等三角形的性质对应边相等,得AD=CE,CD=BE,则DE=AD+BE.
(2)思路同(1),这是第(1)题的变式,实质问题没变。
(3)这是(1)问题的变式,实质问题没变。
【试题解析】
(1)DE=AD+BE.
(2)猜想:(1)中得到的结论发生了变化。
证明:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°.
∴∠BCE+∠CBE=90°.
∵∠ACB=90°,
∴∠ACD+∠BCE=90°.
∴∠ACD=∠CBE.
∵AC=CB,
∴△ACD≌△CBE.
∴AD=CE,CD=BE.
∵DE=CECD,
∴DE=ADBE.
(3)如图3,
猜想:(1)中得到的结论发生了变化。
证明:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°.
∴∠BCE+∠CBE=90°.
∵∠ACB=90°,
∴∠ACD+∠BCE=90°.
∴∠ACD=∠CBE.
∵AC=CB,
∴△ACD≌△CBE.
∴AD=CE,CD=BE.
∵DE=CDCE,
∴DE=BEAD.

练习册系列答案
相关题目