题目内容
【题目】如图，△ABC为等边三角形，AE＝CD，AD、BE相交于点P，BQ⊥AD于Q，PQ＝3，PE＝1．AD的长是（ ）
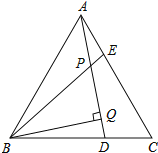
A.5B.6C.7D.8
【答案】C
【解析】
由已知条件，先证明△ABE≌△CAD得∠BPQ=60°，可得BP=2PQ=6，AD=BE．则易求AD的长．
∵△ABC为等边三角形，
∴AB＝CA，∠BAE＝∠ACD＝60°；
又∵AE＝CD，
在△ABE和△CAD中，
，
∴△ABE≌△CAD（SAS）；
∴BE＝AD，∠CAD＝∠ABE；
∴∠BPQ＝∠ABE+∠BAD＝∠BAD+∠CAD＝∠BAE＝60°；
∵BQ⊥AD，
∴∠AQB＝90°，则∠PBQ＝90°﹣60°＝30°；
∵PQ＝3，
∴在Rt△BPQ中，BP＝2PQ＝6；
又∵PE＝1，
∴AD＝BE＝BP+PE＝7．
故选：C．
练习册系列答案
阅读快车系列答案
相关题目
