Question

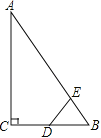
【题目】如图，在△ABC中，∠ACB＝90°，以点B为圆心，BC的长为半径画弧，交线段AB于点D，以点A为圆心，AD长为半径画弧，交线段AC于点E，设BC＝a，AC＝b．

（1）请你判断：线段AD的长度是方程x2+2ax﹣b2＝0的一个根吗？说明理由；

（2）若线段AD＝EC，求的值．

Answer 1

【答案】（1）线段AD的长度是方程x2+2ax﹣b2＝0的一个根，理由详见解析；（2）．

【解析】

（1）方程变形即可得到，根据勾股定理得到，由，即可得到结论；

（2）由题意得，，根据勾股定理列出，整理得到，即可求得．

解：（1）∵在△ABC中，∠ACB＝90°，

∴AB2＝AC2+BC2，

∵BC＝a，AC＝b．

∴AB2＝a2+b2，

方程x2+2ax﹣b2＝0变形为：x2+2ax+a2＝a2+b2，

∴（x+a）2＝AB2，

∵BD＝BC＝a，

∴（x+BD）2＝AB2，

∵（AD+BD）2＝AB2，

∴线段AD的长度是方程x2+2ax﹣b2＝0的一个根；

（2）∵AD＝EC，

∴AC＝2AD＝2AE＝b，

，

，

，

整理得，

．