题目内容
已知直线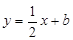 与
与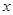 轴交于点A(-4,0),与
轴交于点A(-4,0),与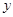 轴交于点B.
轴交于点B.

1.求b的值
2.把△AOB绕原点O顺时针旋转90°后,点A落在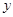 轴的
轴的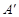 处,点B若在
处,点B若在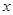 轴的
轴的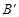 处;
处;
①求直线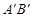 的函数关系式;
的函数关系式;
②设直线AB与直线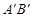 交于点C,矩形PQMN是△
交于点C,矩形PQMN是△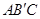 的内接矩形,其中点P,Q在线段
的内接矩形,其中点P,Q在线段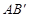 上,点M在线段
上,点M在线段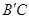 上,点N在线段AC上.若矩形PQMN的两条邻边的比为1∶2,试求矩形PQMN的周长.
上,点N在线段AC上.若矩形PQMN的两条邻边的比为1∶2,试求矩形PQMN的周长.
【答案】
1.2
2.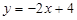 ,8或6
,8或6
【解析】(1)把A(-4,0)代入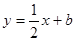 ,得
,得
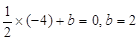
(2)①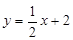 ,令
,令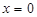 ,得
,得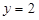 ,∴B(0,2)
,∴B(0,2)
由旋转性质可知
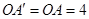 ,
, 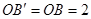
∴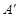 (0,4),
(0,4),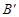 (2,0)
(2,0)
设直线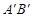 的解析式为
的解析式为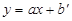
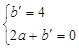 解得
解得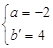 ∴直线
∴直线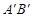 的解析式为
的解析式为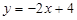
②∵点N在AC上 ∴设N(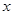 ,
,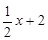 ) (
) (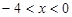 )
)
∵四边形PQMN为矩形 ∴NP=MQ=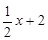
ⅰ)当PN:PQ=1∶2时, PQ=2PN=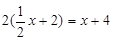
∴ ,0), M(
,0), M(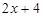 ,
,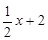 )
)
∵点M在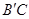 上,
∴
上,
∴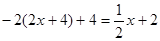
解得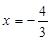 , 此时
, 此时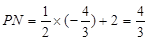 ,PQ=
,PQ=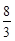
∴矩形PQMN的周长为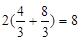
ⅱ)当PN∶PQ=2∶1时, PQ=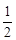 PN=
PN=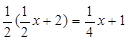
∴Q(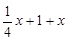 ,0), M(
,0), M(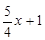 ,
,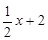 )
)
∵点M在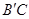 上,∴
上,∴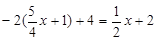
解得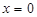 ,此时PN=2,PQ=1
,此时PN=2,PQ=1
∴矩形PQMN的周长为2(2+1)=6
综上所述,当PN∶PQ=1∶2时,矩形PQMN的周长为8
当PQ∶PN =1∶2时,矩形PQMN的周长为6

练习册系列答案
相关题目
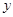 轴交于点B.
轴交于点B.
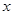 轴的
轴的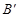 处;
处;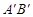 交于点C,矩形PQMN是△
交于点C,矩形PQMN是△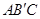 的内接矩形,其中点P,Q在线段
的内接矩形,其中点P,Q在线段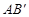 上,点M在线段
上,点M在线段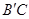 上,点N在线段AC上.若矩形PQMN的两条邻边的比为1∶2,试求矩形PQMN的周长.
上,点N在线段AC上.若矩形PQMN的两条邻边的比为1∶2,试求矩形PQMN的周长.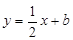 与
与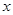 轴交于点A(-4,0),与
轴交于点A(-4,0),与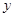 轴交于点B.
轴交于点B.
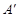 处,点B若在
处,点B若在 处;
处;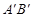 的函数关系式;
的函数关系式;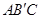 的内接矩形,其中点P,Q在线段
的内接矩形,其中点P,Q在线段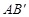 上,点M在线段
上,点M在线段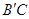 上,点N在线段AC上.若矩形PQMN的两条邻边的比为1∶2,试求矩形PQMN的周长.
上,点N在线段AC上.若矩形PQMN的两条邻边的比为1∶2,试求矩形PQMN的周长.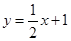 与
与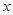 轴交于点
轴交于点 ,与
,与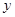 轴交于点
轴交于点 ,将三角形
,将三角形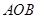 绕点
绕点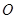 顺时针旋转90°,使点
顺时针旋转90°,使点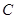 ,点
,点 ,抛物线
,抛物线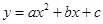 过点
过点 交于点
交于点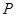 .
.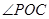 的正切值;
的正切值; 在
在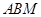 与△
与△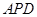 相似,求点
相似,求点
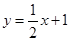 与
与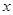 轴交于点
轴交于点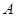 ,与
,与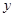 轴交于点
轴交于点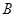 ,将三角形
,将三角形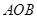 绕点
绕点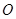 顺时针旋转90°,使点
顺时针旋转90°,使点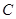 ,点
,点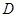 ,抛物线
,抛物线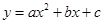 过点
过点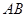 交于点
交于点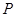 .
. 的正切值;
的正切值;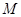 在
在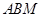 与△
与△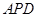 相似,求点
相似,求点