题目内容
已知12+22+32+…+n2=| 1 | 6 |
分析:根据12+22+32+…+1002=22+42+62+…+1002+(12+32+52+…+992),22+42+62+…+1002-(12+32+52+…+992)来求22+42+62+…+1002的值.
解答:解:∵12+22+32+…+n2=
n(n+1)(2n+1),
∴12+22+32+…+1002=22+42+62+…+1002+(12+32+52+…+992)
×100×(100+1)(2×100+1)=338350;
又∵22+42+62+…+1002-(12+32+52+…+992)
=(22-12)+(42-32)+(62-52)+…+(1002-992)
=(2+1)(2-1)+(4-3)(4+3)+(6+5)(6-5)+…+(100+99)(100-99)
=(2+1)+(4+3)+(6+5)+…+(100+99)
=5050;
∴22+42+62+…+1002=
=171700.
故答案为:171700.
| 1 |
| 6 |
∴12+22+32+…+1002=22+42+62+…+1002+(12+32+52+…+992)
| 1 |
| 6 |
又∵22+42+62+…+1002-(12+32+52+…+992)
=(22-12)+(42-32)+(62-52)+…+(1002-992)
=(2+1)(2-1)+(4-3)(4+3)+(6+5)(6-5)+…+(100+99)(100-99)
=(2+1)+(4+3)+(6+5)+…+(100+99)
=5050;
∴22+42+62+…+1002=
| 338350+5050 |
| 2 |
故答案为:171700.
点评:本题主要考查了有理数的乘法,解答此题时,先分组,再利用平方差公式求解.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
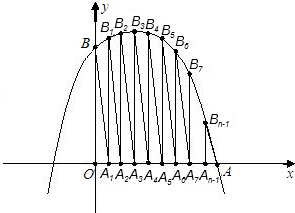 S2、S3、S4、…、Sn.
S2、S3、S4、…、Sn. n(n+1)(2n+1),则22+42+62+…+1002=________.
n(n+1)(2n+1),则22+42+62+…+1002=________.