题目内容
(2002•宜昌)如图,扇形DEF的圆心角∠FDE=90°点D(d,0)在点E的左侧,d为大于0的实数,直线y= x与
x与 交于点M,OM=2(O是坐标原点),以直线DF为对称轴的抛物线y=x2+px+q与x轴交于点E,
交于点M,OM=2(O是坐标原点),以直线DF为对称轴的抛物线y=x2+px+q与x轴交于点E,(1)求点E的坐标;
(2)抛物线y=x2+px+q与x轴的交点有可能都在原点的右侧吗?请说明理由;
(3)设抛物线y=x2+px+q的顶点到x轴的距离为h,求h的取值范围.

【答案】分析:(1)首先根据d的取值范围和直线OM的函数图象确定点M所在的象限,然后设出点M的坐标,利用OM的长和直线OM的解析式,求出点M的坐标,进而可由勾股定理求出DM的长,由于DM、DE都是扇形DEF的半径,因此DM=DE,即可求得DE的值,从而得到点E的坐标.
(2)根据抛物线的对称轴为DF,可用d表示出p的值,然后将E点坐标代入抛物线的解析式中,可用d表示出q的值,进而可得到抛物线的解析式;设抛物线与x轴的两交点的横坐标为x1、x2,由韦达定理可得x1x2的表达式,然后根据d的取值范围来判断x1x2的符号,若x1x2大于0,则说明两个交点有可能都在原点右侧,反之则不能.
(3)首先求出抛物线的顶点坐标,用含d的式子表示出h,即可得关于h、d的函数关系式,结合d的取值范围和函数的性质,即可得到h的取值范围.
解答: 解:(1)过M作MH⊥x轴于H,连接DM,设M(a,b);
解:(1)过M作MH⊥x轴于H,连接DM,设M(a,b);
由于d>0,所以E在x正半轴上,扇形OEF在第一、四象限;
而直线y=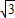 x经过一、三象限,故点M在第一象限;
x经过一、三象限,故点M在第一象限;
∴a>0,b>0,OH=a,MH=b;
由于M在直线y= x上,
x上,
故b= a,而OM=2,即:
a,而OM=2,即:
( a)2+a2=4,
a)2+a2=4,
解得a=1,b=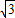 ,
,
即M(1, );
);
∴DM= =
=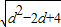 ,
,
∴OE= +d,
+d,
故E(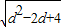 +d,0).
+d,0).
(2)设抛物线与x轴的另一个交点为N;
已知直线DF是抛物线的对称轴,则d=- ,即p=-2d;
,即p=-2d;
将点E坐标代入抛物线的解析式中,得:
(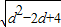 +d)2-2d(
+d)2-2d( +d)+q=0,
+d)+q=0,
整理得:q=2d-4;
即抛物线的解析式为:y=x2-2dx+2d-4;
∵DH=1-d≥0,故0<d≤1,
∴x1x2=q=2d-4<0,
即x1、x2异号,
所以抛物线于x轴两个交点不可能都在原点右侧.
(3)由y=x2-2dx+2d-4=(x-d)2-d2+2d-4,得:
抛物线的顶点坐标为:(d,-d2+2d-4),
又h=|-d2+2d-4|=(d-1)2+3≥3>0,
∴h=d2-2d+4为关于d的二次函数;
在0<d≤1的范围内,h随d的增大而减小,
∴3≤h<4.
点评:此题考查了勾股定理、根与系数的关系、二次函数解析式的确定、二次函数的增减性等知识,综合性强,难度较大.
(2)根据抛物线的对称轴为DF,可用d表示出p的值,然后将E点坐标代入抛物线的解析式中,可用d表示出q的值,进而可得到抛物线的解析式;设抛物线与x轴的两交点的横坐标为x1、x2,由韦达定理可得x1x2的表达式,然后根据d的取值范围来判断x1x2的符号,若x1x2大于0,则说明两个交点有可能都在原点右侧,反之则不能.
(3)首先求出抛物线的顶点坐标,用含d的式子表示出h,即可得关于h、d的函数关系式,结合d的取值范围和函数的性质,即可得到h的取值范围.
解答:
 解:(1)过M作MH⊥x轴于H,连接DM,设M(a,b);
解:(1)过M作MH⊥x轴于H,连接DM,设M(a,b);由于d>0,所以E在x正半轴上,扇形OEF在第一、四象限;
而直线y=
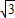 x经过一、三象限,故点M在第一象限;
x经过一、三象限,故点M在第一象限;∴a>0,b>0,OH=a,MH=b;
由于M在直线y=
 x上,
x上,故b=
 a,而OM=2,即:
a,而OM=2,即:(
 a)2+a2=4,
a)2+a2=4,解得a=1,b=
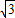 ,
,即M(1,
 );
);∴DM=
 =
=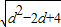 ,
,∴OE=
 +d,
+d,故E(
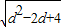 +d,0).
+d,0).(2)设抛物线与x轴的另一个交点为N;
已知直线DF是抛物线的对称轴,则d=-
 ,即p=-2d;
,即p=-2d;将点E坐标代入抛物线的解析式中,得:
(
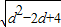 +d)2-2d(
+d)2-2d( +d)+q=0,
+d)+q=0,整理得:q=2d-4;
即抛物线的解析式为:y=x2-2dx+2d-4;
∵DH=1-d≥0,故0<d≤1,
∴x1x2=q=2d-4<0,
即x1、x2异号,
所以抛物线于x轴两个交点不可能都在原点右侧.
(3)由y=x2-2dx+2d-4=(x-d)2-d2+2d-4,得:
抛物线的顶点坐标为:(d,-d2+2d-4),
又h=|-d2+2d-4|=(d-1)2+3≥3>0,
∴h=d2-2d+4为关于d的二次函数;
在0<d≤1的范围内,h随d的增大而减小,
∴3≤h<4.
点评:此题考查了勾股定理、根与系数的关系、二次函数解析式的确定、二次函数的增减性等知识,综合性强,难度较大.

练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 x与
x与 交于点M,OM=2(O是坐标原点),以直线DF为对称轴的抛物线y=x2+px+q与x轴交于点E,
交于点M,OM=2(O是坐标原点),以直线DF为对称轴的抛物线y=x2+px+q与x轴交于点E,

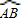 的长.
的长.
