题目内容
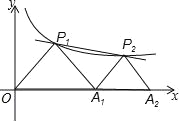
【题目】如图，P1、P2是反比例函数
（k＞0）在第一象限图象上的两点，点A1的坐标为（4，0）．若△P1OA1与△P2A1A2均为等腰直角三角形，其中点P1、P2为直角顶点．
（1）求反比例函数的解析式．
（2）①求P2的坐标．
②根据图象直接写出在第一象限内当x满足什么条件时，经过点P1、P2的一次函数的函数值大于反比例函数的函数值．
【答案】（1）
；（2）①
,②
.
【解析】
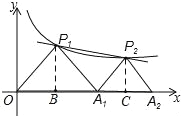
试题分析：（1）过P1做P1B⊥x轴于点B.则P1B=
OA1，OP1=
OA1，则P1可求，反比例函数解析式可求；（2）①过P2做P2C⊥x轴，同（1）可设P2坐标（4+a，a），代入解析式中中求得a值，P2坐标可求.②观察图像可发现当图像在P1P2之间时，一次函数值大于反比例函数值，进而确定x的范围即可.
试题解析：（1）过点P1作P1B⊥x轴，垂足为B.∵点A1的坐标为（4，0），△P1OA1为等腰直角三角形，∴OB=2，P1B=
OA1=2，∴P1的坐标为（2，2）.将P1的坐标代入反比例函数
，得k=2×2=4，∴反比例函数的解析式为.（2）①过点P2作P2C⊥x轴，垂足为C，∵△P2A1A2为等腰直角三角形，∴P2C=A1C.设P2C=A1C=a，则P2的坐标为（4+a，a），将P2的坐标代入反比例函数的解析式，得
，解得
，
（舍去）.∴P2的坐标为（
，
）.②在第一象限内，当
时，一次函数的函数值大于反比例函数的值．
练习册系列答案
相关题目
