题目内容
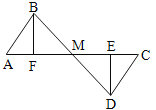
【题目】如图,E、F分别为线段AC上两个动点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC于M.说明:MB=MD,ME=MF.
【答案】证明过程见解析
【解析】
试题分析:根据垂直得出∠DEC=∠BFA=90°,然后结合AB=CD,AF=CE得出Rt△ABF和△Rt△CDE全等,从而得到BF=DE,然后根据∠BFM=∠DEM,∠BMF=∠DME得到△BMF和△DME全等,从而得出答案.
试题解析:因为DE⊥AC,BF⊥AC,所以∠DEC=∠BFA=90°.
又因为AB=CD,AF=CE, 所以Rt△ABF≌Rt△CDE,所以BF=DE.
又因为∠BFM=∠DEM,∠BMF=∠DME, 所以△BMF≌△DME,所以MB=MD,MF=ME.

练习册系列答案
相关题目
