题目内容
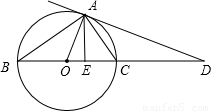
如图，AD切⊙O于A点，BC为直径，连接CA，已知∠ACB=20°，则∠CAD的度数为70°
70°
．分析：首先连接OA，由AD切⊙O于A点，可求得∠OAD的度数，又由OA=OC，即可求得∠OAC的度数，继而求得答案．
解答：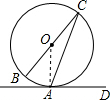
解：连接OA，
∵AD切⊙O于A点，
∴OA⊥AD，
即∠OAD=90°，
∵OA=OC，
∴∠OAC=∠ACB=20°，
∴∠CAD=∠OAD-∠OAC=70°．
故答案为：70°．
解：连接OA，∵AD切⊙O于A点，
∴OA⊥AD，
即∠OAD=90°，
∵OA=OC，
∴∠OAC=∠ACB=20°，
∴∠CAD=∠OAD-∠OAC=70°．
故答案为：70°．
点评：此题考查了切线的性质以及等腰三角形的性质．此题比较简单，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
练习册系列答案
阅读快车系列答案
相关题目
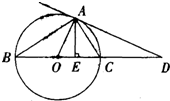23、如图，AD切⊙O于点A，直径BC，交AD于D，AE⊥BD于E．请根据图形将线段成比例的式子写出来（至少写出4个．一个比例式和由它变形得出的比例式按一个计算）．并证明其中的一个比例式成立．
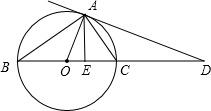如图，AD切⊙O于点A，直径BC，交AD于D，AE⊥BD于E．请根据图形将线段成比例的式子写出来（至少写出4个．一个比例式和由它变形得出的比例式按一个计算）．并证明其中的一个比例式成立．
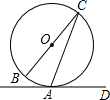如图，AD切⊙O于A点，BC为直径，连接CA，已知∠ACB=20°，则∠CAD的度数为________．