题目内容
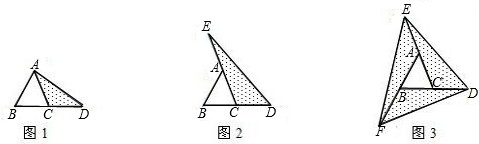
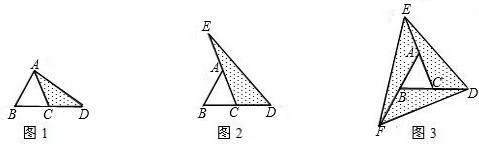
操作与探究探索：在如图1至图3中，△ABC的面积为a．
（1）如图1，延长△ABC的边BC到点D，使CD=BC，连接DA、若△ACD的面积为S1，则S1=
（2）如图2，延长△ABC的边BC到点D，延长边CA到点E，使CD=BC，AE=CA，连接DE、若△DEC的面积为S2，则S2=
（3）在图2的基础上延长AB到点F，使BF=AB，连接FD，FE，得到△DEF（如图3）、若阴影部分的面积为S3，则S3=
发现：像上面那样，将△ABC各边均顺次延长一倍，连接所得端点，得到△DEF（如图3），此时，我们称△ABC向外扩展了一次、可以发现，扩展一次后得到的△DEF的面积是原来△ABC面积的
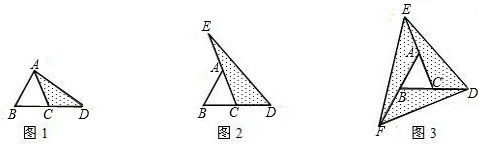
分析：（1）根据等底等高的三角形面积相等解答即可；
（2）分别过A、E作BD的垂线，根据三角形中位线定理及三角形的面积公式求解即可；
（3）由△BFD、△ECD及△AEF的边长为△ABC边长的一半，高与△AEF的高相等解答即可．
（2）分别过A、E作BD的垂线，根据三角形中位线定理及三角形的面积公式求解即可；
（3）由△BFD、△ECD及△AEF的边长为△ABC边长的一半，高与△AEF的高相等解答即可．
解答：解：（1）∵CD=BC，△ABC的面积为a，△ABC与△ACD的高相等，
∴S1=S△ABC=a；
（2）分别过A、E作AG⊥BD，EF⊥BD，G、F为垂足，则AG∥EF，
∵A为CE的中点，∴AG=
EF，
∵BC=CD，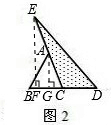
∴S2=2S1=2a；
（3）∵△BDF的边长BD是△ABC边长BC的2倍，两三角形的两边互为另一三角形两边的延长线，
∴S△BDF=2S△ABC，
∵△ABC面积为a，∴S△BDF=2a．
同理可得，S△ECD=2a，S△AEF=2a，∴S3=S△BDF+S△ECD+S△AEF=2a+2a+2a=6a．
∵S3=S△BDF+S△ECD+S△AEF=6a，
∴S△EDF=S3+S△ABC=6a+a=7a，
∴
=
=7，
∴扩展一次后得到的△DEF的面积是原来△ABC面积的7倍．
∴S1=S△ABC=a；
（2）分别过A、E作AG⊥BD，EF⊥BD，G、F为垂足，则AG∥EF，
∵A为CE的中点，∴AG=
| 1 |
| 2 |
∵BC=CD，
∴S2=2S1=2a；
（3）∵△BDF的边长BD是△ABC边长BC的2倍，两三角形的两边互为另一三角形两边的延长线，
∴S△BDF=2S△ABC，
∵△ABC面积为a，∴S△BDF=2a．
同理可得，S△ECD=2a，S△AEF=2a，∴S3=S△BDF+S△ECD+S△AEF=2a+2a+2a=6a．
∵S3=S△BDF+S△ECD+S△AEF=6a，
∴S△EDF=S3+S△ABC=6a+a=7a，
∴
| S△DEF |
| S△ABC |
| 7a |
| a |
∴扩展一次后得到的△DEF的面积是原来△ABC面积的7倍．
点评：本题比较复杂，只要根据三角形的面积公式进行分析即可．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
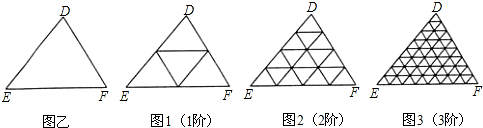
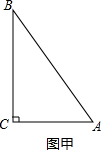定义：若某个图形可分割为若干个都与他相似的图形，则称这个图形是自相似图形．
