题目内容
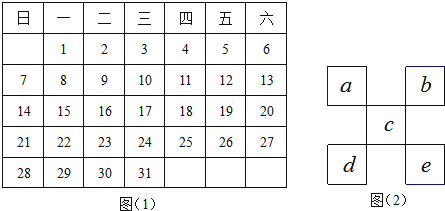
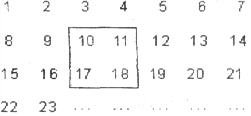
【题目】把正整数1,2,3,4,……,2009排列成如图所示的一个表
(1)用一正方形在表中随意框住4个数,把其中最小的数记为x,另三个数用含x的式子表示出来,从小到大依次是 , , 。
(2)当被框住的4个数之和等于416时,x的值是多少?
(3)被框住的4个数之和能否等于622?如果能,请求出此时x的值;如果不能,请说明理由。
【答案】(1)从小到大依次是x+1、x+7、x+8。(2)100;(3)不能,理由见解析.
【解析】试题分析:(1)根据上下两个数相差7,左右两个数相差1,分别表示出结果即可;
(2)利用四个数的和为416列出方程解答即可;
(3)利用四个数的和为622列出方程解答,求得整数解可以,否则不可能.
试题解析:(1)从小到大依次是x+1、x+7、x+8。
(2)由题意可得:
x+(x+1)+(x+7)+(x+8)=416
4x+16=416
x=100
所以,x的值为100。
(3)不能。理由如下:
x+(x+1)+(x+7)+(x+8)=622
4x+16=622
x=![]()
因为x为正整数,所以框出的四个数的和不能为622。

【题目】从2开始,连续的偶数相加,它们和的情况如下表:
加数的个数n | S |
1 | 2=1×2 |
2 | 2+4=6=2×3 |
3 | 2+4+6=12=3×4 |
4 | 2+4+6+8=20=4×5 |
5 | 2+4+6+8+10=30=5×6 |
(1)若n=8时,则S的值为_____________.
(2)根据表中的规律猜想:用n的式子表示S的公式为:S=2+4+6+8+…+2n=__________________.
(3)根据上题的规律计算2+4+6+8+10+…+98+100![]() 的值.
的值.
【题目】某报社为了了解市民“获取新闻的最主要途径”,开展了一次抽样调查,根据调查结果绘制了如下三种不完整的统计图表.
组别 | 获取新闻的最主要途径 | 人数 |
| 电脑上网 | 280 |
| 手机上网 |
|
| 电视 | 140 |
| 报纸 |
|
| 其他 | 80 |
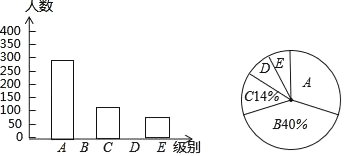
请根据图表信息解答下列问题:
(1)统计表中的![]() ,
,![]() ,并请补全条形统计图;
,并请补全条形统计图;
(2)扇形统计图中“![]() ”所对应的圆心角的度数是 ;
”所对应的圆心角的度数是 ;
(3)若该市约有100万人,请你估计其中将“电脑上网”和“手机上网”作为“获取新闻的最主要途径”的总人数.