题目内容
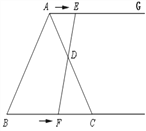
【题目】如图,在正方形ABCD中,点E为边AB上任一点(与点A,B不重合),连接CE,过点D作DF⊥CE于点F,连接AF并延长交BC边于点G,连接EG,若正方形边长为4,GC=![]() AE,则GE= .
AE,则GE= .
【答案】![]()
![]() .
.
【解析】
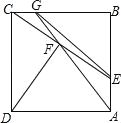
试题分析:如图,延长DA、CE交于点M.假设AE=3a,GC=2a,想办法用a的代数式表示AM、CF、FM,由![]() =
=![]() ,列出方程即可解决问题.如图,延长DA、CE交于点M.
,列出方程即可解决问题.如图,延长DA、CE交于点M.
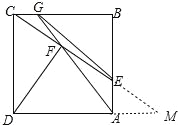
∵GC=![]() AE,可以假设AE=3a,GC=2a,∵四边形ABCD 是正方形,AB=BC=CD=AD=4,AB∥CD,BC∥AD,∴
AE,可以假设AE=3a,GC=2a,∵四边形ABCD 是正方形,AB=BC=CD=AD=4,AB∥CD,BC∥AD,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴AM=
,∴AM=![]() ,由△CDF∽△ECB,得
,由△CDF∽△ECB,得![]() =
=![]() ,∴CF=
,∴CF=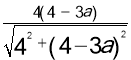 ,由△MDF∽△CEB,得
,由△MDF∽△CEB,得![]() =
=![]() ,∴FM=
,∴FM=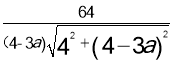 ,∵CG∥AM,∴
,∵CG∥AM,∴![]() =
=![]() ,∴
,∴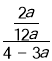 =
=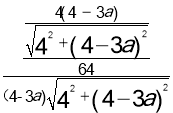 ,解得a=
,解得a=![]() ,在Rt△GBE中,∵BG=4﹣
,在Rt△GBE中,∵BG=4﹣![]() =
=![]() ,BE=4﹣
,BE=4﹣![]() =
=![]() ,∴GE=
,∴GE=![]() =
=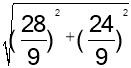 =
=![]()
![]() ,故答案为
,故答案为![]()
![]() .
.

练习册系列答案
相关题目
【题目】七年级学生完成课题学习“从数据谈节水”后,积极践行“节约用水,从我做起”,现在从七年级400名学生中选出10名学生统计各自家庭一个月的节水情况如下表:
节水量(m3) | 0.2 | 0.25 | 0.3 | 0.4 | 0.5 |
家庭数 | 1 | 2 | 2 | 4 | 1 |
那么这组数据的众数和平均数分别是( )
A. 0.4m3和0.34m3 B. 0.4m3和0.3m3 C. 0.25m3和0.34m3 D. 0.25m3和0.3m3