��Ŀ����
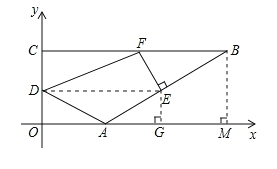
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A(![]() ��0)��B(3
��0)��B(3![]() ��2)��C��0��2)������D��ÿ��1����λ���ٶ�
��2)��C��0��2)������D��ÿ��1����λ���ٶ�
�ӵ�0������OC���յ�C�˶���ͬʱ����E��ÿ��2����λ���ٶȴӵ�A������AB���յ�B�˶�������E��EF��AB����BC�ڵ�F������DA��DF�����˶�ʱ��Ϊt�룮
(1)���ABC�Ķ�����
(2)��tΪ��ֵʱ��AB��DF��
(3)���ı���AEFD�����ΪS��
����S����t�ĺ�����ϵʽ��
����һ������y=x2+mx��������E����S<2![]() ʱ����m��ȡֵ��Χ(д���𰸼���)��
ʱ����m��ȡֵ��Χ(д���𰸼���)��

���𰸡�(1)30o;(2) ![]() ;(3)
;(3) ![]()
![]()
�������������������1�����ABC�Ķ��������BAx�Ķ�������B��BM��x����M����AM=2![]() ��BM=2���ɴ˿ɵó���BAM����ABC�Ķ�����
��BM=2���ɴ˿ɵó���BAM����ABC�Ķ�����
��2����AB��FDʱ����CFD=��B=30�㣬����ֱ��������CDF�У���CD�ij���ʾ��CF��ͬ������ֱ��������FEB�У���BE�ij���ʾ��BF��Ȼ��ɸ���CF+BF=BC�����t��ֵ��
��3��������DE������D��E���ٶȿ�֪AE=2OD����AE=2EG�����OD��=EG�����ı���ODEG�Ǿ��Σ����DE��x�ᣬ��ô�ı���AEFD������ɷֳ�������ADE��������EFD��������������������ζ���DEΪ�ף��������θߵĺ�������OC�ij�������ı���ADEF������͵���![]() DEOC���ؼ������DE�ij��������A��DE�Ĵ��߲��ѵó�DE=OA+AEsin60�㣬�ɴ˿ɵó�S��t�ĺ�����ϵʽ��
DEOC���ؼ������DE�ij��������A��DE�Ĵ��߲��ѵó�DE=OA+AEsin60�㣬�ɴ˿ɵó�S��t�ĺ�����ϵʽ��
����֪��S��ȡֵ��Χ�ɸ��ݢٵĺ�����ϵʽ���t��ȡֵ��Χ���ڢ����Ѿ������E�����꣬������������ߵĽ���ʽ�У���m��ʾ��t��ֵ��Ȼ�����t��ȡֵ��Χ�������m��ȡֵ��Χ��
���������
��1������B��BM��x���ڵ�M
��C��0��2����B��![]() ��
��
��BC��OA
���ABC=��BAM
��BM=2��AM=![]()
��tan��BAM=![]()
���ABC=��BAM=30�㣮
��2����AB��DF
���CFD=��CBA=30��
��Rt��DCF�У�CD=2-t����CFD=30�㣬
��CF=![]() ��2-t��
��2-t��
��AB=4��
��BE=4-2t����FBE=30�㣬
��BF=![]()
��![]()
��t=![]()
��3��������DE������E��EG��x���ڵ�G��
��EG=t��OG=![]() t+
t+![]()
��E(![]() t+
t+![]() ,t)
,t)
��DE��x��
S=S��DEF+S��DEA=![]() DE��CD+
DE��CD+![]() DE��OD
DE��OD
=![]() t+
t+![]()
�ڵ�S��![]() ʱ��
ʱ��
�ɢٿ�֪��S=![]() t+
t+![]()
��![]() t+
t+![]() <
<![]()
��t��1��
��t��0��
��0��t��1��
��y=-x2+mx����E(![]() t+
t+![]() ,t)
,t)
��t=0ʱ��E��![]() ,0��
,0��
��m=![]()
��t=1ʱ��E��![]() ,1��
,1��
��m=![]()
��![]()