Question

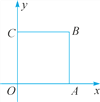
【题目】如图，在平面直角坐标系中，正方形OABC的一个顶点为B(1，1)，点A，C分别在x轴，y轴上．

(1)点A的坐标为______，点C的坐标为_______．

(2)判断直线y＝－2x＋与正方形OABC是否有交点，并说明理由．

(3)将直线y＝－2x＋进行平移，恰好能把正方形OABC分成面积相等的两部分，请求出平移后的直线的函数表达式．

Answer 1

【答案】(1)(1,0),(0,1);(2)有，理由见解析；（3）y＝－2x＋

【解析】试题分析：（1）利用正方形的性质，可得A,C的坐标. （2）求出y＝－2x＋与坐标轴的交点，易得结论.(3)要想平分正方形的面积，直线必须通过正方形的中心，所以求出正方形的中心坐标，代入平移的直线方程可得所求.

试题解析：（1）利用正方形的性质，可得A(1,0),C（0,1）.

(2)有．理由如下：

把x＝0代入y＝－2x＋，得y＝；

把y＝0代入y＝－2x＋，得－2x＋＝0，解得x＝.

∴直线y＝－2x＋与坐标轴的交点为和.

∵OC＝1，OA＝1，∴直线与正方形有交点．

(3)设平移后的直线的函数表达式为y＝－2x＋b.

根据题意，易得直线y＝－2x＋b应经过AC与BO的交点，即过正方形OABC的中心点.

把点的坐标代入y＝－2x＋b，得－2×＋b＝，解得b＝.

∴所求直线的函数表达式为y＝－2x＋.