题目内容
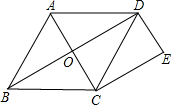 如图,O是菱形ABCD对角线的交点,作DE∥AC,CE∥BD,DE、CE交于点E.
如图,O是菱形ABCD对角线的交点,作DE∥AC,CE∥BD,DE、CE交于点E.
(1)四边形OCDE是矩形吗?说说你的理由;
(2)请你将上述条件中的菱形改为另一种四边形,其它条件都不变,你能得出什么结论?根据改编后的题目画出图形,并说明理由.
解:(1)四边形OCDE是矩形.
证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
又∵AC⊥BD,
∴∠DOC=90°,
∴四边形OCED是矩形.
(2)任意改变四边形ABCD的形状,四边形OCED都是平行四边形(答案不唯一).
理由如下:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形.
分析:(1)由菱形的性质可证AC⊥BD,∠DOC=90°,又已知DE∥AC,CE∥BD,可证四边形OCED是平行四边形,所以四边形OCED是矩形;
(2)由已知DE∥AC,CE∥BD,所以四边形OCED是平行四边形.
点评:本题考查菱形的性质、矩形的判定和平行四边形的判定.
证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
又∵AC⊥BD,
∴∠DOC=90°,
∴四边形OCED是矩形.
(2)任意改变四边形ABCD的形状,四边形OCED都是平行四边形(答案不唯一).
理由如下:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形.
分析:(1)由菱形的性质可证AC⊥BD,∠DOC=90°,又已知DE∥AC,CE∥BD,可证四边形OCED是平行四边形,所以四边形OCED是矩形;
(2)由已知DE∥AC,CE∥BD,所以四边形OCED是平行四边形.
点评:本题考查菱形的性质、矩形的判定和平行四边形的判定.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
 ( )
( ) 时,菱形ABCD的边长为2.
时,菱形ABCD的边长为2.
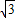 时,菱形ABCD的边长为2.
时,菱形ABCD的边长为2.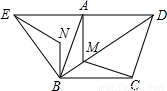
 时,菱形ABCD的边长为2.
时,菱形ABCD的边长为2.
 时,菱形ABCD的边长为2.
时,菱形ABCD的边长为2.