Question

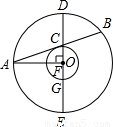
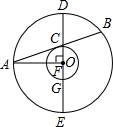已知：如图，在以O为圆心的两个同心圆中，大圆的弦AB和小圆相切于点C，过点C作大圆的弦DE，使DE⊥OA，垂足为F，DE交小圆于另一点G．求证：AF•AO=DC•DG．

Answer 1

分析：连接OC，根据相交弦定理可得，AC•BC=DC•CE，又AB是小圆的切线，故OC⊥AB，根据垂径定理，可得AC=BC，故AC²=DC•CE；又因为OC⊥AB，DE⊥OA，所以有∠AFC=∠ACO=90°，且∠CAF=∠OAC，那么△ACF∽△AOC，可得比例线段AC：AF=AO：AC，即AC²=AO•AF；于是有AO•AF=DC•CE；而DE⊥OA，利用垂径定理，可得DF=EF，CF=FG，等量加等量和相等，可得DG=CE，等量代换可得AO•AF=DC•DG．

解答：证明：连接OC，（1分）
∵AB是小圆切线，
∴OC⊥AB，
∴AC=BC，（1分）
∵AB与DE相交于C，
∴CA•CB=CD•CE，（1分）
∴AC²=CD•CE，①
∵OC⊥AC，CF⊥OA，
∴△ACO∽△AFC，
∴

AC

AF

=

AO

AC

，
∴AC²=AF•AO，②
∵OF⊥DE，
∴CF=GF，DF=EF，
∴DF+FG=EF+CF，
∴DG=EC，③（2分）
由①、②、③，可得AF•AO=DC•DG．

点评：本题利用了垂径定理、相似三角形的判定和性质、相交弦定理、等量代换等知识．