题目内容
解方程或不等式(组)
(1)
+1≥x并把解集在数轴上表示出来.
(2)
并把解集在数轴上表示出来.
(3)解分式方程:
+3=
(4)解分式方程:
=
-
.
(1)
| x-1 |
| 2 |
(2)
|
(3)解分式方程:
| 1 |
| x-2 |
| x-1 |
| x-2 |
(4)解分式方程:
| x-2 |
| x-3 |
| 1 |
| 2 |
| x+3 |
| 9-x2 |
分析:(1)先去分母得到x-1+2≥2x,然后再移项、合并、系数化为1即可;再在数轴上表示解集;
(2)分别解两个不等式得到x≥-1和x<2,然后根据大于小的小于大的取中间即可得到不等式组的解集,再在数轴上表示解集;
(3)方程两边都乘以(x-2)得到1+3(x-2)=x-1,解得x=2,然后进行检验确定分式方程的解;
(3)先把方程变形、化简得到
=
+
,再把方程两边都乘以(x-3)得到2(x-2)=x-3+2,解得x=3,然后进行检验确定分式方程的解.
(2)分别解两个不等式得到x≥-1和x<2,然后根据大于小的小于大的取中间即可得到不等式组的解集,再在数轴上表示解集;
(3)方程两边都乘以(x-2)得到1+3(x-2)=x-1,解得x=2,然后进行检验确定分式方程的解;
(3)先把方程变形、化简得到
| x-2 |
| x-3 |
| 1 |
| 2 |
| 1 |
| x-3 |
解答:解:(1)去分母得x-1+2≥2x,
移项得x-2x≥1-2,
合并得-x≥-1,
系数化为1得x≤1,
在数轴上表示解集如下: ;
;
(2)
,
解①得x≥-1,
解②得x<2,
∴-1≤x<2,
 ;
;
(3)去分母得1+3(x-2)=x-1,
解得x=2,
检验:当x=2时,x-2=0,所以x=2是原方程的增根,
所以原方程无解;
(4)方程变形为:
=
+
,
化简得:
=
+
,
去分母得2(x-2)=x-3+2,
解得x=3,
检验:当x=3时,2(x-3)=0,所以x=3是原方程的增根,
所以原方程无解.
移项得x-2x≥1-2,
合并得-x≥-1,
系数化为1得x≤1,
在数轴上表示解集如下:
 ;
;(2)
|
解①得x≥-1,
解②得x<2,
∴-1≤x<2,
 ;
;(3)去分母得1+3(x-2)=x-1,
解得x=2,
检验:当x=2时,x-2=0,所以x=2是原方程的增根,
所以原方程无解;
(4)方程变形为:
| x-2 |
| x-3 |
| 1 |
| 2 |
| x+3 |
| (x-3)(x+3) |
化简得:
| x-2 |
| x-3 |
| 1 |
| 2 |
| 1 |
| x-3 |
去分母得2(x-2)=x-3+2,
解得x=3,
检验:当x=3时,2(x-3)=0,所以x=3是原方程的增根,
所以原方程无解.
点评:本题考查了解分式方程:先把分式方程化为整式方程,解整式方程,然后进行检验,把整式方程的解代入分式方程的分母中,若分母为零,则这个整式方程的解为分式方程的增根;若分母不为零,则这个整式方程的解为分式方程的解.也考查了解一元一次不等式以及一元一次不等式组.

练习册系列答案
相关题目
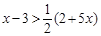 (2)
(2)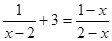
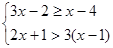 ,并把解集在数轴上表示出来
,并把解集在数轴上表示出来 (2)
(2)
 ,并把解集在数轴上表示出来
,并把解集在数轴上表示出来