题目内容
解方程或不等式(组):(1)(1-2x)2+9=6(1-2x)
(2)
|
分析:(1)利用不等式的基本性质即可求得原不等式的解集;
(2)分别求解两个不等式,然后求出两个不等式的解集的公共部分即可.
(2)分别求解两个不等式,然后求出两个不等式的解集的公共部分即可.
解答:(1)解:(1-2x)2-6(1-2x)+9=0
即(1-2x-3)2=0(2分)
∴1-2x-3=0(1分)
解得:x1=x2=-1(1分)
(2)解:解(1)得:y>-2
解(2)得:y<1
∴原不等式组的解集为:-2<y<1
即(1-2x-3)2=0(2分)
∴1-2x-3=0(1分)
解得:x1=x2=-1(1分)
(2)解:解(1)得:y>-2
解(2)得:y<1
∴原不等式组的解集为:-2<y<1
点评:本题考查了解不等式和方程,注意:解不等式时,移项要变号,系数化为1时,若是负系数,不等号的方向要改变.

练习册系列答案
相关题目
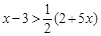 (2)
(2)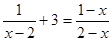
 ,并把解集在数轴上表示出来
,并把解集在数轴上表示出来 (2)
(2)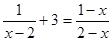
 ,并把解集在数轴上表示出来
,并把解集在数轴上表示出来