题目内容
有一个测量弹跳力的体育器材,如图所示,竖杆AC、BD的长度分别为200厘米、300厘米,CD=300厘米.现有一人站在斜杆AB下方的点E处,直立、单手上举时中指指尖(点F)到地面的高度为EF,屈膝尽力跳起时,中指指尖刚好触到斜杆AB上的点G处,此时,就将EG与EF的差值y(厘米)作为此人此次的弹跳成绩.设CE=x(厘米),EF=a(厘米).
(1)问点G比点A高出多少厘米?(用含y,a的式子表示)
(2)求出由x和a算出y的计算公式;
(3)现有甲、乙两组同学,每组三人,每人各选择一个适当的位置尽力跳了一次,且均刚好触到斜杆,由所得公式算得两组同学弹跳成绩如下右表所示,由于某种原因,甲组C同学的弹跳成绩辨认不清,但知他弹跳时的位置为x=150厘米,且a=205厘米,请你计算C同学此次的弹跳成绩,并从两组同学弹跳成绩的整齐程度比较甲、乙两组同学的弹跳成绩.
(方差计算公式:S2=
[(x1-
)2+(x2-
)2+…+(xn-
)2],其中
表示x1、x2、…、xn的平均数)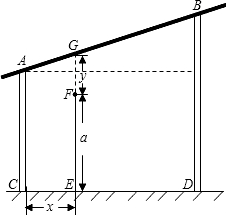
(1)问点G比点A高出多少厘米?(用含y,a的式子表示)
(2)求出由x和a算出y的计算公式;
(3)现有甲、乙两组同学,每组三人,每人各选择一个适当的位置尽力跳了一次,且均刚好触到斜杆,由所得公式算得两组同学弹跳成绩如下右表所示,由于某种原因,甲组C同学的弹跳成绩辨认不清,但知他弹跳时的位置为x=150厘米,且a=205厘米,请你计算C同学此次的弹跳成绩,并从两组同学弹跳成绩的整齐程度比较甲、乙两组同学的弹跳成绩.
| 甲组 | 乙组 | |||||
| A同学 | B同学 | C同学 | a同学 | b同学 | C同学 | |
| 弹跳成绩(厘米) | 36 | 39 | 42 | 44 | 34 | |
| 1 |
| n |
| . |
| x |
| . |
| x |
| . |
| x |
| . |
| x |

(1)过A作AM⊥BD于点M,交GE于N,
∵AC⊥CD,GE⊥CD,
∴四边形ACEN为矩形.
∴NE=AC.
又∵AC=200,EF=a,FG=y,
∴GN=GE-NE=a+y-200.
即点G比点A高出(a+y-200)厘米.
(2)∵DM=AC=200,
∴BM=BD-DM=300-200=100.
∵GN∥BM,
∴△ANG∽△AMB.AM=CD=300,
∴
=
,即
=
.
∴y=
x-a+200.
(3)当x=150cm,a=205cm时,y=
×150-205+200=45(cm).
即甲组C同学的弹跳成绩为45cm.
∵
甲=
(36+39+45)=40,
=
(42+44+34)=40,
∴S甲2=
[(36-40)2+(39-40)2+(45-40)2]=14,
S乙2=
[(42-40)2+(44-40)2+(34-40)2]=
.
∴S甲2<S乙2,即甲组同学的弹跳成绩更整齐.

∵AC⊥CD,GE⊥CD,
∴四边形ACEN为矩形.
∴NE=AC.
又∵AC=200,EF=a,FG=y,
∴GN=GE-NE=a+y-200.
即点G比点A高出(a+y-200)厘米.
(2)∵DM=AC=200,
∴BM=BD-DM=300-200=100.
∵GN∥BM,
∴△ANG∽△AMB.AM=CD=300,
∴
| AN |
| AM |
| GN |
| BM |
| x |
| 300 |
| a+y-200 |
| 100 |
∴y=
| 1 |
| 3 |
(3)当x=150cm,a=205cm时,y=
| 1 |
| 3 |
即甲组C同学的弹跳成绩为45cm.
∵
| . |
| x |
| 1 |
| 3 |
| . |
| x乙 |
| 1 |
| 3 |
∴S甲2=
| 1 |
| 3 |
S乙2=
| 1 |
| 3 |
| 56 |
| 3 |
∴S甲2<S乙2,即甲组同学的弹跳成绩更整齐.


练习册系列答案
相关题目