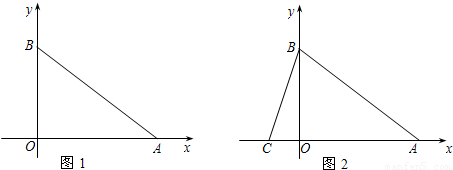题目内容
已知:一张直角三角形纸片如图1放置在平面直角坐标系中,一条直角边OA落在x轴正半轴上,另一条直角边OB落在y轴正半轴上,且OA=8,OB=6.现再找一个与Rt△ABO有一条公共边且不重叠的三角形,使它们拼在一起后能构成一个大的等腰三角形.例如:如图2,△CBO与△ABO拼成等腰△ABC,则点C坐标为(-2,0).请直接写出除图2情况外,其他所有的所拼成的等腰三角形中除A、B、O三点外另一顶点P的坐标.
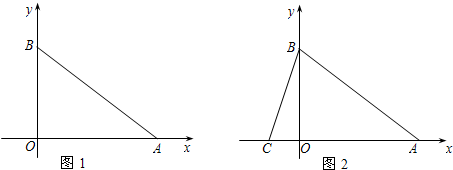
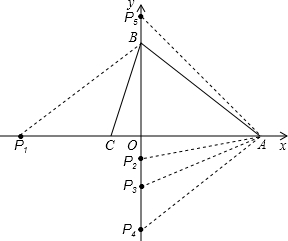 解:∵OA=8,OB=6,
解:∵OA=8,OB=6,∴AB=
 =
= =10,
=10,①重合边是OB时,PB=AB,则OP=OA=8,
所以,点P的坐标为(-8,0),
②重合边是OA时,若BP=AP,则OA2+OP2=AP2=BP2,
即82+OP2=(6+OP)2,
解得OP=
 ,
,所以,点P的坐标为(0,-
 );
);若BP=AB,则OP=10-6=4,
所以,点P的坐标为(0,-4);
若AP=AB,则OP=OB=6,
所以,点P的坐标为(0,-6);
③重合边是AB时,OP=OA=8,
所以,点P的坐标为(0,8);
综上所述,点P的坐标为(-8,0),(0,-
 ),(0,-4),(0,-6),(0,8).
),(0,-4),(0,-6),(0,8).分析:先根据勾股定理求出AB,再分重合边为OB、OA、AB时三种情况作出图形,然后求出相应的点P的坐标即可.
点评:本题考查了等腰三角形的判定,坐标与图形的性质,勾股定理的应用,难点在于要分情况讨论,作出图形更形象直观.

练习册系列答案
相关题目
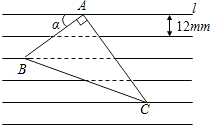 如图,把一张直角三角形卡片ABC放在每格宽度为12mm的横格纸中,三个顶点恰好都落在横格线上,已知∠BAC=90°,∠α=36°,求直角三角形卡片ABC的面积(精确到1mm).(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
如图,把一张直角三角形卡片ABC放在每格宽度为12mm的横格纸中,三个顶点恰好都落在横格线上,已知∠BAC=90°,∠α=36°,求直角三角形卡片ABC的面积(精确到1mm).(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
 已知:如图,小明把一张直角三角形的硬纸片像图中那样折叠,使得A与B重合,小明看到硬纸片上标着AB=20cm,请你猜猜CE的长是
已知:如图,小明把一张直角三角形的硬纸片像图中那样折叠,使得A与B重合,小明看到硬纸片上标着AB=20cm,请你猜猜CE的长是