题目内容
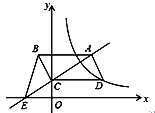
【题目】如图,平行四边形ABCD的顶点C在y轴正半轴上,CD平行于x轴,直线AC交x轴于点E,BC⊥AC,连接BE,反比例函数![]() (x>0)的图象经过点D.已知S△BCE=1,则k的值是( )
(x>0)的图象经过点D.已知S△BCE=1,则k的值是( )
A. 2 B. ﹣2 C. 3 D. 4
【答案】D
【解析】连接ED、OD,由平行四边形的性质可得出BC=AD,AD⊥AC,根据同底等高的三角形面积相等即可得出S△BCE=S△DCE,同理得出S△OCD=S△DCE,再利用反比例函数系数K几何意义即可求出结论.
解:连接ED、OD,如图所示,

∵四边形ABCD为平行四边形,
∴BC=AD,BC∥AD,
∵BC⊥AC,
∴AD⊥AC,
∵S△BCE和S△DCE有相同的底CE,相等的高BC=AD,
∴S△OCD=S△DCE,
∵CD平行于x轴,
∴△OCD与△ECD有相等的高,
∴S△OCD=S△DCE=S△BCE=2=![]() ,
,
∴![]() ,
,
∵反比例函数在第一象限有图象,
∴![]() ,
,
故选:D.
“点睛”本题考查了反比例函数系数K何意义、平行四边形的性质以及平行线的性质,利用同底等高的三角形面积相等找出S△OCD=S△DCE=S△BCE是解题的关键.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目