Question

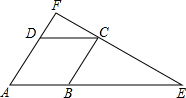（2012•龙岩模拟）如图，在菱形ABCD中，延长AB到点E，使BE=2AB，连接EC并延长交AD的延长线于点F．
（1）求证：△DFC∽△AFE；
（2）若AE=9，求线段AF的长．

Answer 1

分析：（1）由菱形的性质：DC∥AE，进而证明：△DFC∽△AFE；
（2）由（1）可知：△DFC∽△AFE，利用相似三角形的性质和已知条件即可求出DF的长，进而求出AF的长．

解答：（1）证明：∵四边形ABCD是菱形，
∴DC∥AE，
∴△DFC∽△AFE；
（2）解：∵△DFC∽△AFE；
∴

DF

AF

=

DC

AE

，
∵BE=2AB，AE=9，
∴BE=6，AB=3，
∴

DF

3+DF

=

3

9

，
∴DF=

3

2

．
∴AF=AD+DF=3+

3

2

=4.5．

点评：本题考查了菱形的性质，相似三角形的判定和性质，题目的难度不大，属于基础性题目．