题目内容
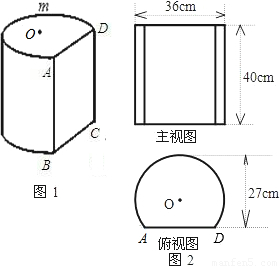
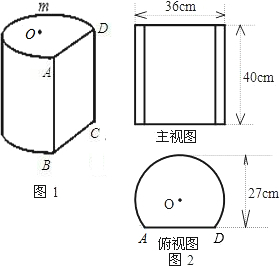
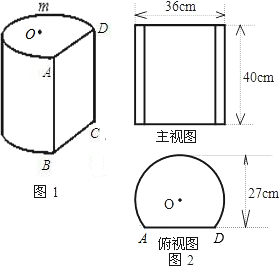如图，图1是过圆柱体木块底面的一条弦AD，沿母线AB剖开后得到的柱体，剖面是矩形ABCD，O为原圆柱体木块底面的圆心．图2是该柱体的主视图和俯视图．请你根据图中标注的数据解决以下问题．
（1）求弦AD的长度；
（2）求这个柱体的表面积．（结果可保留π和根号）
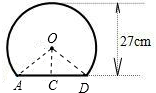解：（1）作OC⊥AD于点C，连接OD，则△OCD是直角三角形．易得OD=36÷2=18cm，OC=27-18=9cm，
∴CD=9
cm，∴AD=2CD=18
cm；（2）由（1）易得∠COD=60°，那么∠AOD=120°，
∴两个上下底面的面积之和为：2[
+
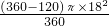×18×9]=512π+162（cm2）；侧面积之和为：18
×40+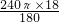
×40=720+960π（cm2）；∴这个柱体的表面积为1472π+882
=（cm2）．分析：（1）由主视图和俯视图易得直径长为主视图中的宽36cm，构造半径所在的直角三角形求得AD的一半后乘2即为AD长，
（2）柱体的表面积=侧面积+上下底面的面积．
点评：主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形；难点是利用勾股定理得到弦AD的一半，以及∠AOD的度数．
练习册系列答案
相关题目
如图，图1是过圆柱体木块底面的一条弦AD，沿母线AB剖开后得到的柱体，剖面是矩形ABCD，O为原圆柱体木块底面的圆心．图2是该柱体的主视图和俯视图．请你根据图中标注的数据解决以下问题．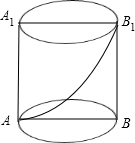
如图：有一圆柱体高为8πcm，底面圆的半径为6cm，AA1、BB1为相对的两条母线，在点A处有一个蜘蛛，点B处有一只苍蝇，蜘蛛沿圆柱体侧面爬到B1处吃掉苍蝇，问蜘蛛所爬过的最短路径长是多少？
把一个类似于圆柱体的蛋糕放在水平桌面上，用一把类似于平面的刀竖直去切这个蛋糕（如图）．（1）开始一刀切得的截面是什么图形？
（2）切一刀成2块，切二刀成4块，切三刀、四刀呢？最多可切得多少块蛋糕？根据事实填写下列表格：
| 所切刀数 | 0 | 1 | 2 | 3 | 4 | 5 | … |
| 得到蛋糕块数 | … |
