题目内容
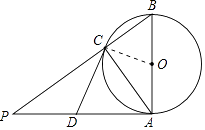
【题目】如图,AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C,点D为AP的中点,连结AC.求证: 
(1)∠P=∠BAC
(2)直线CD是⊙O的切线.
【答案】
(1)解:证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACP=90°,
∴∠P+∠CAP=90°,
∵AP⊙O是切线,
∴∠BAP=90°,
即∠CAP+∠BAC=90°
∴∠P=∠BAC;
(2)解:∵CD是Rt△PAC斜边PA的中线,
∴CD=AD,
∴∠DCA=∠DAC,
连接OC,
∵OC=OA,
∴∠OCA=∠OAC,
∴∠DCO=∠DAO=90°,
∴CD是⊙O的切线.
【解析】(1)要证明∠P=∠BAC,只要证明∠CAP+∠BAC=∠P+∠CAP即可,根据题目中的条件可以证明它们相等,从而可以解答本题;(2)要证明直线CD是⊙O的切线,只要证明∠OCD=90°即可,根据题目中的条件和(1)中的结论可以证明∠OCD=90°,从而可以解答本题.

练习册系列答案
相关题目







