题目内容
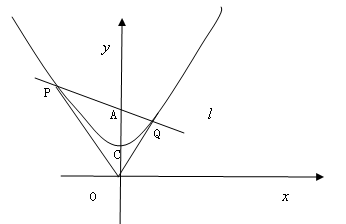
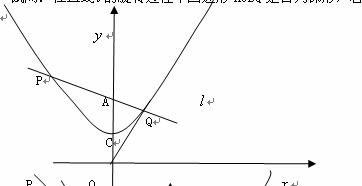
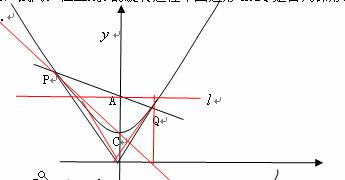
如图,点O为坐标原点,直线![]() 绕着点A(0,2)旋转,与经过点C(0,1)的二次函数
绕着点A(0,2)旋转,与经过点C(0,1)的二次函数![]()
![]() 交于不同的两点P、Q.
交于不同的两点P、Q.
(1).求h的值;
(2).通过操作、观察算出△POQ面积的最小值;
(3).过点P、C作直线,与![]() 轴交于点B,试问:在直线
轴交于点B,试问:在直线![]() 的旋转过程中四边形AOBQ是否为梯形,若是,请说明理由;若不是,请指明其形状.
的旋转过程中四边形AOBQ是否为梯形,若是,请说明理由;若不是,请指明其形状.
(1).0,1)带入二次函数![]()
![]() 中,得
中,得![]() ;
;
(2). 操作、观察可知当直线![]() ∥
∥![]() 轴时,其面积最小;
轴时,其面积最小;
将y=2带入二次函数![]()
![]() 中,得
中,得![]() ,
,
S最小=(2×4)÷2=4.
(3)由特殊到一般:
一、如图①所示,当直线![]() ∥
∥![]() 轴时,四边形AOBQ为正方形。
轴时,四边形AOBQ为正方形。
可知BO=AQ=2;∠AOB=90°,故四边形AOBQ为正方形。
二、如图二,当直线![]() 不平行与
不平行与![]() 轴时,四边形AOBQ为梯形。
轴时,四边形AOBQ为梯形。
连接BQ,设P(![]() ), Q(
), Q(![]() );(
);(![]() )
)
直线BC:![]() 过低点P,即
过低点P,即![]() ,得
,得![]() ;
;
![]() ;点B为(
;点B为(![]() );同理直线
);同理直线![]() :
:![]() ;
;
![]() ;
;![]() ;得b=
;得b=![]() ;
;
所以点Q、P同横坐标,即为AC∥BQ,且AQ不与OB平行;
故四边形AOBQ为梯形。

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案
相关题目
 如图,点O为坐标原点,点A(2n,0)在x轴正半轴,将点A绕点O逆时针旋转60°得到点B,作△OAB,点P是△OAB的重心.将点P绕坐标原点逆时针旋转90°得到点P′,则点P′的坐标是
如图,点O为坐标原点,点A(2n,0)在x轴正半轴,将点A绕点O逆时针旋转60°得到点B,作△OAB,点P是△OAB的重心.将点P绕坐标原点逆时针旋转90°得到点P′,则点P′的坐标是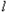 绕着点A(0,2)旋转,与经过点C(0,1)的二次函数
绕着点A(0,2)旋转,与经过点C(0,1)的二次函数
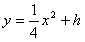 交于不同的两点P、Q
交于不同的两点P、Q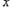 轴交于点B,试问:在直线
轴交于点B,试问:在直线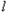 的旋转过程中四边形AOBQ是否为梯形,若是,请说明理由;若不是,请指明其形状
的旋转过程中四边形AOBQ是否为梯形,若是,请说明理由;若不是,请指明其形状