题目内容
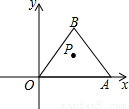
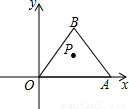
 如图,点O为坐标原点,点A(2n,0)在x轴正半轴,将点A绕点O逆时针旋转60°得到点B,作△OAB,点P是△OAB的重心.将点P绕坐标原点逆时针旋转90°得到点P′,则点P′的坐标是
如图,点O为坐标原点,点A(2n,0)在x轴正半轴,将点A绕点O逆时针旋转60°得到点B,作△OAB,点P是△OAB的重心.将点P绕坐标原点逆时针旋转90°得到点P′,则点P′的坐标是分析:从已知可以判断三角形OAB是正三角形,而正三角形三心合一,可得出∠AOP的度数,平的横坐标是n,根据正切定理可求P的纵坐标,如图可知P的横坐标与P′纵坐标相等,P的纵坐标与P′横坐标互为相反数,由此可得到P′的坐标.
解答:解:如图,连接点PP′、OP、OP′,
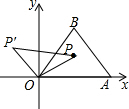
将点A绕点O逆时针旋转60°得到点B,所以△OAB是正三角形,
点P是△OAB的重心,正三角形三心合一,所以OP也是∠AOB的角平分线,
P点的横坐标为:n,
P的纵坐标为:n•tan30°=
n,
△OPP′是一个等腰直角三角形,OP与x轴成30度角,
那么OP′与y轴成30度角,
∴P′的坐标为:(-
n,n).

将点A绕点O逆时针旋转60°得到点B,所以△OAB是正三角形,
点P是△OAB的重心,正三角形三心合一,所以OP也是∠AOB的角平分线,
P点的横坐标为:n,
P的纵坐标为:n•tan30°=
| ||
| 3 |
△OPP′是一个等腰直角三角形,OP与x轴成30度角,
那么OP′与y轴成30度角,
∴P′的坐标为:(-
| ||
| 3 |
点评:本题考查了坐标中图形的旋转变化,正三角形和等腰直角三角形的相关性质.

练习册系列答案
相关题目
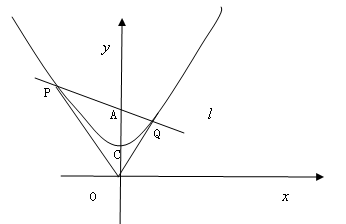
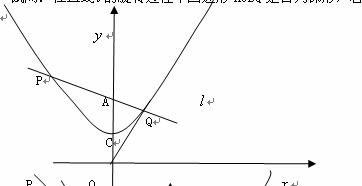
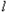 绕着点A(0,2)旋转,与经过点C(0,1)的二次函数
绕着点A(0,2)旋转,与经过点C(0,1)的二次函数
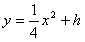 交于不同的两点P、Q
交于不同的两点P、Q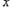 轴交于点B,试问:在直线
轴交于点B,试问:在直线 的旋转过程中四边形AOBQ是否为梯形,若是,请说明理由;若不是,请指明其形状
的旋转过程中四边形AOBQ是否为梯形,若是,请说明理由;若不是,请指明其形状