题目内容
(10分)
如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
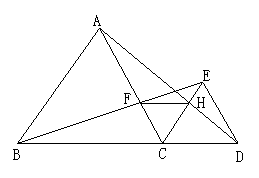
(1)求证:△BCE≌△ACD;
(2)求证:FH‖BD.
证明略
解析:(1)证明:∵△ABC和△CDE都是等边三角形
∴BC=AC,CE=CD,∠BCA=∠ECD=60°
∴∠BCA+∠ACE=∠ECD+∠ACE即∠BCE=∠ACD
∴在△BCE和△ACD中, 
∴△BCE≌△ACD (SAS).
(2)证法一:由(1)知△BCE≌△ACD,∴∠CBF=∠CAH,BC=AC
又∵△ABC和△CDE都是等边三角形,且点B、C、D在同一条直线上
∴∠ACH=180°-∠ACB-∠HCD=60°=∠BCF
∴在△BCF和△ACH中, 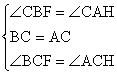
∴△BCF≌△ACH (ASA)
∴CF=CH又∵∠FCH=60°∴△CHF为等边三角形
∴∠FHC=∠HCD=60°∴FH‖BD
(证法二,本题也可由△CFE≌△CHD(ASA)得出△CHF为等边三角形)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

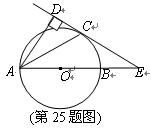
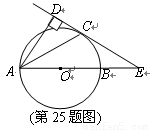
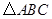 ,以
,以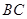 为直径,
为直径,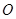 为圆心的半圆交
为圆心的半圆交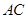 于点
于点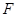 ,点
,点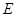 为弧CF的中点,连接
为弧CF的中点,连接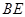 交
交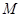 ,
,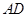 为△ABC的角平分线,且
为△ABC的角平分线,且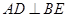 ,垂足为点
,垂足为点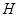 . [来源:]
. [来源:]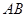 是半圆
是半圆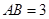 ,
,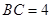 ,求
,求