题目内容
（11·柳州）（本题满分10分）如图，已知AB是⊙O的直径，锐角∠DAB的平分线AC交⊙O于点C，作CD⊥AD，垂足为D，直线CD与AB的延长线交于点E．
（1）求证：直线CD为⊙O的切线；
（2）当AB＝2BE，且CE＝时，求AD的长．
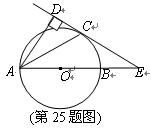
src="http://thumb.1010pic.com/pic1/imagenew2/czsx/15/78955.gif" >【答案】解：(1)连接OC
∵AC平分∠DAB
∴∠DAC＝∠CAB
∵OA＝OC
∴∠OCA＝∠CAB
∴∠OCA＝∠DAC
∴AD∥CO
∵CD⊥AD
∴CD⊥AD
∴CD为⊙O的切线
（2）∵AB＝2BO AB＝2BE
∴BO＝BE＝CO
设BO＝BE＝CO＝x
∴OE＝2x
在Rt△OCE中，
OC2＋CE2＝OE2
x2＋()2＝(2x)2
∴x＝1
∴AE＝3 ∠E＝30°
AD＝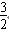
解析:
略
∵AC平分∠DAB
∴∠DAC＝∠CAB
∵OA＝OC
∴∠OCA＝∠CAB
∴∠OCA＝∠DAC
∴AD∥CO
∵CD⊥AD
∴CD⊥AD
∴CD为⊙O的切线
（2）∵AB＝2BO AB＝2BE
∴BO＝BE＝CO
设BO＝BE＝CO＝x
∴OE＝2x
在Rt△OCE中，
OC2＋CE2＝OE2
x2＋()2＝(2x)2
∴x＝1
∴AE＝3 ∠E＝30°
AD＝
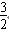解析:略
练习册系列答案
相关题目
