题目内容
如图为中华人民共和国国旗上的一个五角星，同学们再熟悉不过了，那么它的每个角的度数为（ ）| A、45° | B、30° | C、36° | D、40° |
分析：五角星中间的部分五边形ABCDE是正五边形，根据内角和定理即可求得每个内角的度数，△ABM是等腰三角形，根据三角形内角和定理即可求得五角星的每个角的度数．
解答：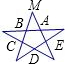
解：正五边形ABCDE的内角和是（5-2）•180=540°．
∴∠ABC=∠BAE=
=108°．
∴∠MBA=∠MAB=180-108=72°
∴在△MAB中，∠M=180-72-72=36°．
则五角星的每个角的度数为36°．
故选C．
解：正五边形ABCDE的内角和是（5-2）•180=540°．∴∠ABC=∠BAE=
| 540 |
| 5 |
∴∠MBA=∠MAB=180-108=72°
∴在△MAB中，∠M=180-72-72=36°．
则五角星的每个角的度数为36°．
故选C．
点评：本题主要考查了多边形的内角和的计算方法，正确理解五边形ABCDE是正五边形是解决本题的关键．
练习册系列答案
相关题目
4、如图是国庆庆祝的活动标志，它以数学“60”为主体，代表着中华人民共和国60年光辉历程．画中左侧小圆与右侧优弧所在的大圆之间的位置关系是（ ）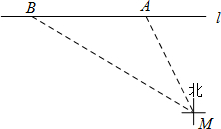
（2012•高淳县一模）《中华人民共和国道路交通管理条理》规定：“小汽车在城市街道公路上的行驶速度不得超过70km/h（即19.44m/s）”．如图所示，已知测速站M到街道公路l的距离为90m，一辆小汽车在街道公路l上由东向西行驶，测得此车从点A行驶到点B所用的时间为6s，并测得A在M的北偏西27°方向上，B在M的北偏西60°方向上．求出此车从A到B的平均速度，并判断此车是否超过限速．
如图为中华人民共和国国旗上的一个五角星，同学们再熟悉不过了，那么它的每个角的度数为