题目内容
（2009•青岛）一根水平放置的圆柱形输水管道横截面如图所示，其中有水部分水面宽0.8米，最深处水深0.2米，则此输水管道的直径是（ ）
A．0.4米
B．0.5米
C．0.8米
D．1米
【答案】分析：根据题意知，已知弦长和弓形高，求半径（直径）．根据垂径定理和勾股定理求解．
解答：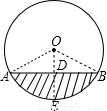
解：设半径为r，过O作OE⊥AB交AB于点D，连接OA、OB，
则AD=
AB=
×0.8=0.4米，
设OA=r，则OD=r-DE=r-0.2，
在Rt△OAD中，
OA2=AD2+OD2，即r2=0.42+（r-0.2）2，解得r=0.5米，
故此输水管道的直径=2r=2×0.5=1米．
故选D．
点评：此题涉及圆中求半径的问题，此类在圆中涉及弦长、半径、圆心角的计算的问题，常把半弦长，半圆心角，圆心到弦距离转换到同一直角三角形中，然后通过直角三角形予以求解，常见辅助线是过圆心作弦的垂线．
解答：
解：设半径为r，过O作OE⊥AB交AB于点D，连接OA、OB，则AD=
| 1 |
| 2 |
| 1 |
| 2 |
设OA=r，则OD=r-DE=r-0.2，
在Rt△OAD中，
OA2=AD2+OD2，即r2=0.42+（r-0.2）2，解得r=0.5米，
故此输水管道的直径=2r=2×0.5=1米．
故选D．
点评：此题涉及圆中求半径的问题，此类在圆中涉及弦长、半径、圆心角的计算的问题，常把半弦长，半圆心角，圆心到弦距离转换到同一直角三角形中，然后通过直角三角形予以求解，常见辅助线是过圆心作弦的垂线．
练习册系列答案
智慧课堂密卷100分单元过关检测系列答案
相关题目
-50，30）
-50）
，30）
）