题目内容
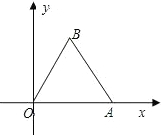 如图,边长为2的等边三角形OAB的顶点A在x轴的正半轴上,B点位于第一象限,将△OAB绕点O顺时针旋转30°后,恰好点A落在双曲线y=
如图,边长为2的等边三角形OAB的顶点A在x轴的正半轴上,B点位于第一象限,将△OAB绕点O顺时针旋转30°后,恰好点A落在双曲线y=| k | x |
分析:如图,等边三角形OAB顺时针旋转30°后AB⊥x轴,因此D就是AB与x轴的交点,那么可得出AD=1,OD=
,那么A点的坐标就是(
,-1),因此反比例函数的k=xy=-
,如果要想使再一次旋转后A仍在反比例函数上,那么就必须满足k=x•y=-
,那么满足这样条件的离第一次旋转后A点最近的点就应该是(1,-
),而此时∠AOx的度数为60°,由此即可得到至少要再顺时针旋转的度数.
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
解答:解:如图,∵等边三角形OAB顺时针旋转30°,
∴AB⊥x轴,
∴D就是AB与x轴的交点,
而三角形的边长为2,
∴AD=1,OD=
,
∴A点的坐标就是(
,-1),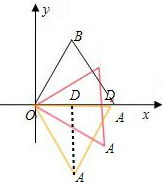
∴反比例函数的k=xy=-
,
如果要想使再一次旋转后A仍在反比例函数上,
那么新的A(x,y)就必须满足x•y=-
,
∴满足这样条件的离第一次旋转后A点最近的点就应该是(1,-
),
而此时∠AOx的度数为60°,
因此至少要再顺时针旋转30°,才能使A点落到反比例函数上.
故答案为:30.
∴AB⊥x轴,
∴D就是AB与x轴的交点,
而三角形的边长为2,
∴AD=1,OD=
| 3 |
∴A点的坐标就是(
| 3 |

∴反比例函数的k=xy=-
| 3 |
如果要想使再一次旋转后A仍在反比例函数上,
那么新的A(x,y)就必须满足x•y=-
| 3 |
∴满足这样条件的离第一次旋转后A点最近的点就应该是(1,-
| 3 |
而此时∠AOx的度数为60°,
因此至少要再顺时针旋转30°,才能使A点落到反比例函数上.
故答案为:30.
点评:本题主要考查了等边三角形的性质,反比例函数的应用以及旋转的相关知识,先根据第一次旋转后A点的坐标来确定反比例函数的解析式是解题的关键所在.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
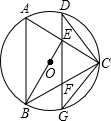 如图,边长为4的等边三角形ABC内接于⊙O,直线EF经过边AC,BC的中点,交⊙O于D、G两点.
如图,边长为4的等边三角形ABC内接于⊙O,直线EF经过边AC,BC的中点,交⊙O于D、G两点.
 (1997•南京)已知:如图,边长为2的等边三角形ABC,延长BC到D,使CD=BC,延长CB到E,使BE=CB,求△ADE的周长.
(1997•南京)已知:如图,边长为2的等边三角形ABC,延长BC到D,使CD=BC,延长CB到E,使BE=CB,求△ADE的周长. (2013•福州质检)如图,边长为6的等边三角形ABC中,E是对称轴AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF.则在点E运动过程中,DF的最小值是
(2013•福州质检)如图,边长为6的等边三角形ABC中,E是对称轴AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF.则在点E运动过程中,DF的最小值是