题目内容
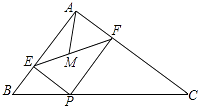
【题目】如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠B=65°,则∠1的度数是( ) 
A.45°
B.25°
C.20°
D.15°
【答案】C
【解析】解:在Rt△ABC中,∵∠B=65°, ∴∠BAC=90°﹣65°=25°,
∵Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,
∴∠ACA′=90°,∠B′A′C=∠BAC=20°,CA=CA′,
∴△CAA′为等腰直角三角形,
∴∠CA′A=45°,
∴∠1=∠CA′A﹣∠B′A′C=45°﹣25°=20°,
故选C.
先利用互余计算出∠BAC=90°﹣70°=20°,再根据旋转的性质得∠ACA′=90°,∠B′A′C=∠BAC=20°,CA=CA′,则可判断△CAA′为等腰直角三角形得到∠CA′A=45°,然后计算∠CA′A﹣∠B′A′C即可.

练习册系列答案
 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目