题目内容
半径分别是2，4，6的三圆两两外切，那么以这三个圆的圆心为顶点的三角形的形状是
- A.钝角三角形
- B.等腰三角形
- C.锐角三角形
- D.直角三角形
D
分析：根据两圆外切，则圆心距等于两圆半径之和，可以求得三角形的三边，再根据勾股定理的逆定理即可判断三角形是直角三角形．
解答：∵半径分别是2，4，6的三圆两两外切，
∴以这三个圆的圆心为顶点的三角形的三边分别是2+4=6，2+6=8，4+6=10．
则有62+82=102，
故该三角形是直角三角形．
故选D．
点评：此题考查了两圆的位置关系与数量之间的联系以及勾股定理的逆定理的运用．
分析：根据两圆外切，则圆心距等于两圆半径之和，可以求得三角形的三边，再根据勾股定理的逆定理即可判断三角形是直角三角形．
解答：∵半径分别是2，4，6的三圆两两外切，
∴以这三个圆的圆心为顶点的三角形的三边分别是2+4=6，2+6=8，4+6=10．
则有62+82=102，
故该三角形是直角三角形．
故选D．
点评：此题考查了两圆的位置关系与数量之间的联系以及勾股定理的逆定理的运用．
练习册系列答案
相关题目
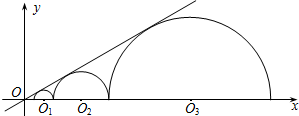半圆C1、半圆C2、半圆C3的半径分别是r1、r2、r3，则当r1=1时，r3=