题目内容
已知:抛物线y=ax2+x+2.(1)当对称轴为x=
| 1 | 2 |
(2)若代数式-x2+x+2的值为正整数,求x的值.
分析:(1)根据抛物线的对称轴为x=-
,求出a的值,然后把解析式写成顶点坐标式求出顶点坐标,
(2)若代数式-x2+x+2的值为正整数,即(1)中的二次函数y=-x2+x+2的函数值y为正整数,求出y的最大值,然后解方程,求出x的值.
| 1 |
| 2 |
(2)若代数式-x2+x+2的值为正整数,即(1)中的二次函数y=-x2+x+2的函数值y为正整数,求出y的最大值,然后解方程,求出x的值.
解答:解:(1)∵对称轴为x=
,∴-
=
.
∵b=1,∴a=-1.
∴此抛物线的解析式为y=-x2+x+2.
顶点坐标为(
,
).
(2)∵代数式-x2+x+2的值为正整数,
即(1)中的二次函数y=-x2+x+2的函数值y为正整数.
由(1)知,y的最大值是
,∴符合题意的y值有:2和1.
∴当y=2时,有-x2+x+2=2.解得x1=0或x2=1;
当y=1时,有-x2+x+2=1.解得x1=
或x2=
.
即所求的x的值为0,1,
,
.
| 1 |
| 2 |
| b |
| 2a |
| 1 |
| 2 |
∵b=1,∴a=-1.
∴此抛物线的解析式为y=-x2+x+2.
顶点坐标为(
| 1 |
| 2 |
| 9 |
| 4 |
(2)∵代数式-x2+x+2的值为正整数,
即(1)中的二次函数y=-x2+x+2的函数值y为正整数.
由(1)知,y的最大值是
| 9 |
| 4 |
∴当y=2时,有-x2+x+2=2.解得x1=0或x2=1;
当y=1时,有-x2+x+2=1.解得x1=
1+
| ||
| 2 |
1-
| ||
| 2 |
即所求的x的值为0,1,
1+
| ||
| 2 |
1-
| ||
| 2 |
点评:本题主要考查待定系数法求二次函数的解析式、二次函数的性质和最值的知识点,熟练掌握二次函数的图象特征和函数的性质是解答本题的关键,本题难度一般.

练习册系列答案
相关题目
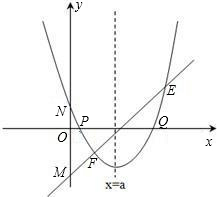 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由. (2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.
(2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.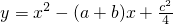 ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边. ,抛物线与x轴交于点P、Q,问是否
,抛物线与x轴交于点P、Q,问是否 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由. ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边.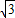 ,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.