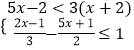题目内容
【题目】对于一个平面图形,通过两种不同的方法计算它的面积,可以得到一个关于整式乘法的等式.例如:计算左图的面积可以得到等式(a+b)(a+2b)=a2+3ab+2b2.
请解答下列问题:
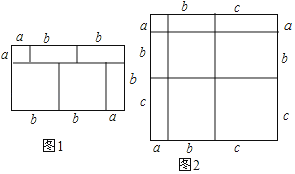
(1)观察如图,写出所表示的等式: = ;
(2)已知上述等式中的三个字母a,b,c可取任意实数,若a=7x﹣5,b=﹣4x+2,c=﹣3x+4,且a2+b2+c2=37,请利用(1)所得的结论求ab+bc+ac的值
【答案】(1)(a+b+c)2,a2+b2+c2+2ab+2bc+2ac;(2)﹣18.
【解析】
(1)从图形的面积可分析出式子;(2)根据2ab+2bc+2ac=(a+b+c)2﹣(a2+b2+c2),代入可得结果.
(1)由图形可得等式:(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;
故答案为:(a+b+c)2,a2+b2+c2+2ab+2bc+2ac;
(2)∵a=7x﹣5,b=﹣4x+2,c=﹣3x+4,且a2+b2+c2=37,
∴2ab+2bc+2ac=(a+b+c)2﹣(a2+b2+c2)
=(7x﹣5﹣4x+2﹣3x+4)2﹣37
=12﹣37
=1﹣37
=﹣36.
∴ab+bc+ac=﹣18.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目