题目内容
直角坐标系中,△OAB的顶点O(0,0),B(-3,0),且∠AOB=45°,将△OAB绕点O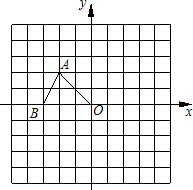 按顺时针方向旋转90°得到△OA'B'.
按顺时针方向旋转90°得到△OA'B'.
(1)画出△OA'B'.
(2)点B'坐标为________.
(3)求BB'的长.
 解:(1)如图所示:△OA′B′.
解:(1)如图所示:△OA′B′.(2)解点B′的坐标是(0,3),
故答案为:(0,3).
(3)解:OB=3,OB′=3,∠BOB′=90°,
由勾股定理得:BB′=
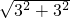 =3
=3 ,
,答:BB′的长是3
 .
.分析:(1)根据点的坐标标出旋转后的对应点,连接即可;
(2)根据旋转的旋转即可求出答案;
(3)由已知和作图得到B、B′的坐标,根据勾股定理求出即可.
点评:本题主要考查对作图-与旋转变换,坐标与图形变换-对称,勾股定理等知识点的理解和掌握,能正确画图和计算是解此题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 到折痕EF.
到折痕EF.
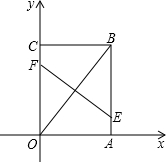
 如图,边长为4的正方形OABC放置在平面直角坐标系中,OA在x轴正半轴上,OC在y轴正半轴上,当直线y=-x+b中的系数b从0开始逐渐变大时,直线在正方形上扫过的面积记为S.则S关于b的函数图象是( )
如图,边长为4的正方形OABC放置在平面直角坐标系中,OA在x轴正半轴上,OC在y轴正半轴上,当直线y=-x+b中的系数b从0开始逐渐变大时,直线在正方形上扫过的面积记为S.则S关于b的函数图象是( )


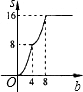
 把矩形OABC放在平面直角坐标系中,OA,OC分别放在x轴、y轴的正半轴上,O为坐标原点,已知OA=4,OC=2,沿直线OB将△OAB翻折,点A落在该平面直角坐标系中的D处,则经过D点的双曲线的解析式为
把矩形OABC放在平面直角坐标系中,OA,OC分别放在x轴、y轴的正半轴上,O为坐标原点,已知OA=4,OC=2,沿直线OB将△OAB翻折,点A落在该平面直角坐标系中的D处,则经过D点的双曲线的解析式为 如图,边长为2的正方形OABC放置在平面直角坐标系中,OA在x轴正半轴上,OC在y轴正半轴上,当直线y=kx的系数k从0开始逐渐变大时,直线在正方形上扫过的面积为记为S,则S关于k的函数图象是( )
如图,边长为2的正方形OABC放置在平面直角坐标系中,OA在x轴正半轴上,OC在y轴正半轴上,当直线y=kx的系数k从0开始逐渐变大时,直线在正方形上扫过的面积为记为S,则S关于k的函数图象是( )