题目内容
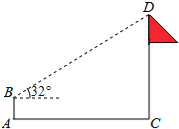
【题目】已知正方形ABCD的边长为4,一个以点A为顶点的45°角绕点A旋转,角的两边分别与BC、DC的延长线交于点E、F,连接EF,设CE=a,CF=b.
(1)如图1,当a=![]() 时,求b的值;
时,求b的值;
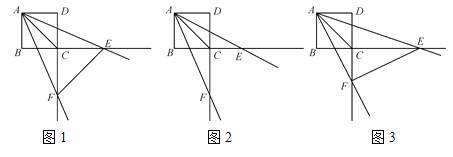
(2)当a=4时,在图2中画出相应的图形并求出b的值;
(3)如图3,请直接写出∠EAF绕点A旋转的过程中a、b满足的关系式.
【答案】(1)![]() ;(2)b=8;(3)ab=32.
;(2)b=8;(3)ab=32.
【解析】
试题(1)由正方形ABCD的边长为4,可得AC=4![]() ,∠ACB=45°.
,∠ACB=45°.
再CE=a=4![]() ,可得∠CAE=∠AEC,从而可得∠CAF的度数,既而可得 b=AC;
,可得∠CAE=∠AEC,从而可得∠CAF的度数,既而可得 b=AC;
(2)通过证明△ACF∽△ECA,即可得;
(3)通过证明△ACF∽△ECA,即可得.
试题解析:(1)∵正方形ABCD的边长为4,∴AC=4![]() ,∠ACB=45°.
,∠ACB=45°.
∵CE=a=4![]() ,∴∠CAE=∠AEC=
,∴∠CAE=∠AEC=![]() =22.5°,∴∠CAF=∠EAF-∠CAE=22.5°,∴∠AFC=∠ACD-∠CAF=22.5°,∴∠CAF=∠AFC,∴b=AC=CF=
=22.5°,∴∠CAF=∠EAF-∠CAE=22.5°,∴∠AFC=∠ACD-∠CAF=22.5°,∴∠CAF=∠AFC,∴b=AC=CF=![]() ;
;
(2)∵∠FAE=45°,∠ACB=45°,∴∠FAC+∠CAE=45°,∠CAE+∠AEC=45°,∴∠FAC=∠AEC.
又∵∠ACF=∠ECA=135°,∴△ACF∽△ECA,∴![]() ,∴
,∴![]() ,∴CF=8,即b=8.
,∴CF=8,即b=8.
(3)ab=32.
提示:由(2)知可证△ACF∽△ECA,∴∴![]() ,∴
,∴![]() ,∴ab=32.
,∴ab=32.

【题目】某种机器使用期为三年,买方在购进机器时,可以给各台机器分别一次性额外购买若干次维修服务,每次维修服务费为2000元.每台机器在使用期间,如果维修次数未超过购机时购买的维修服务次数,每次实际维修时还需向维修人员支付工时费500元;如果维修次数超过机时购买的维修服务次数,超出部分每次维修时需支付维修服务费5000元,但无需支付工时费某公司计划购实1台该种机器,为决策在购买机器时应同时一次性额外购买几次维修服务,搜集并整理了100台这种机器在三年使用期内的维修次数,整理得下表;
维修次数 | 8 | 9 | 10 | 11 | 12 |
频率(台数) | 10 | 20 | 30 | 30 | 10 |
(1)以这100台机器为样本,估计“1台机器在三年使用期内维修次数不大于10”的概率;
(2)试以这100机器维修费用的平均数作为决策依据,说明购买1台该机器的同时应一次性额外购10次还是11次维修服务?