题目内容
(2012•和平区模拟)图①至图③中,两平行线AB、CD间的距离均为6,点M为AB上一定点.扇形纸片OMP在AB、CD之间(包括AB、CD),扇形OMP的圆心角∠MOP=α,半径OM=4.如图①,扇形的半径OM在AB上.如图②③,将扇形纸片OMP绕点M在AB、CD之间顺时针旋转.
(Ⅰ)如图②,当α=60°时,在旋转过程中,点P到直线CD的最小距离是
(Ⅱ)如图③,在扇形纸片OMP旋转的过程中,要使点P落在直线CD上,α的最大值是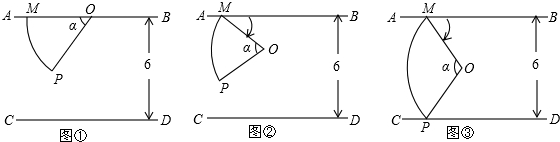
(Ⅰ)如图②,当α=60°时,在旋转过程中,点P到直线CD的最小距离是
2
2
,旋转角∠BMO的最大值是90°
90°
;(Ⅱ)如图③,在扇形纸片OMP旋转的过程中,要使点P落在直线CD上,α的最大值是
120°
120°
.
分析:(I)当PM⊥AB时,点P到AB的距离最大,此时点P到CD的距离最小,求出MP的长度后即可得出点P到直线CD的最小距离;当扇形MOP在AB,CD之间旋转到不能再转时,弧MP与AB相切,此时旋转角最大,也可求出最大值.
(II)点P是弧MP与CD的切点时,α最大,根据解直角三角形的知识,求出∠MOH的度数,继而可得出α的最大值.
(II)点P是弧MP与CD的切点时,α最大,根据解直角三角形的知识,求出∠MOH的度数,继而可得出α的最大值.
解答:解:(I)∵α=60°,
∴△MOP是等边三角形,
∴MO=MP=4,
∴PM⊥AB时,点P到AB的最大距离是4,
由已知得出M与P的距离为4,
从而点P到CD的最小距离为6-4=2,
当扇形MOP在AB,CD之间旋转到不能再转时,弧MP与AB相切,
此时旋转角最大,∠BMO的最大值为90°;
(II)点P是弧MP与CD的切点时,α最大,即OP⊥CD,
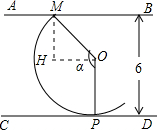
∵OM=OP=4,
∴HM=2,
在RT△HMO中,OM=4,HM=2,
∴∠MOH=30°,
此时α=∠MOH+∠HOP=30°+90°=120°.
故答案为:2、90°;120°.
∴△MOP是等边三角形,
∴MO=MP=4,
∴PM⊥AB时,点P到AB的最大距离是4,
由已知得出M与P的距离为4,
从而点P到CD的最小距离为6-4=2,
当扇形MOP在AB,CD之间旋转到不能再转时,弧MP与AB相切,
此时旋转角最大,∠BMO的最大值为90°;
(II)点P是弧MP与CD的切点时,α最大,即OP⊥CD,

∵OM=OP=4,
∴HM=2,
在RT△HMO中,OM=4,HM=2,
∴∠MOH=30°,
此时α=∠MOH+∠HOP=30°+90°=120°.
故答案为:2、90°;120°.
点评:此题属于圆的综合题,涉及了切线的性质定理以及平行线之间的关系和解直角三角形等知识,根据切线的性质求解是初中阶段的重点题型,此题考查知识较多综合性较强,注意认真分析.

练习册系列答案
相关题目

