题目内容
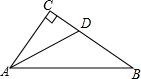
如图：E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，垂足为C，D．
求证：（1）OC=OD；（2）DF=CF．
求证：（1）OC=OD；（2）DF=CF．
证明：（1）∵E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，
∴EC=DE，∠ECO=∠EDO=90°，
在Rt△COE和Rt△DOE中，
，
∴Rt△COE≌Rt△DOE（HL），
∴CO=DO；
（2）∵EO平分∠AOB，
∴∠AOE=∠BOE，
在△COF和△DOF中，
，
∴△COF≌△DOF（SAS），
∴FC=FD．
∴EC=DE，∠ECO=∠EDO=90°，
在Rt△COE和Rt△DOE中，
|
∴Rt△COE≌Rt△DOE（HL），
∴CO=DO；
（2）∵EO平分∠AOB，
∴∠AOE=∠BOE，
在△COF和△DOF中，
|
∴△COF≌△DOF（SAS），
∴FC=FD．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
相关题目
