题目内容
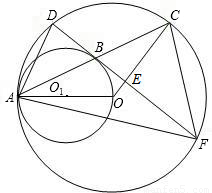
(2003•泰州)已知:如图,⊙O与⊙O1内切于点A,AO是⊙O1的直径,⊙O的弦AC交⊙O1于点B,弦DF经过点B且垂直于OC,垂足为点E.(1)求证:DF与⊙O1相切;
(2)求证:2AB2=AD•AF;
(3)若AB=
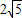 ,cos∠DBA=
,cos∠DBA=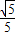 ,求AF和AD的长.
,求AF和AD的长.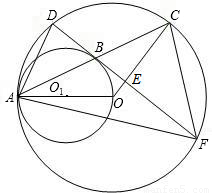
【答案】分析:(1)本题可连接O1B,证O1B⊥DF即可,由于OC⊥DF,因此只需证O1B∥OC即可.可通过不同圆中圆的半径对应的角相等来求得,由此可得证.
(2)本题可通过证△ABD和△AFC相似来求解.连接OB,则OB⊥AC,因此可根据垂径定理得出AC=2AB,那么通过两三角形相似得出的AD:AC=AB:AF,即可得出所求的结论.
(3)本题可先求出BF的长,然后根据相似三角形FCB和ACF得出的CF 2=CB•CA,求出CF的长,还是这两个相似三角形,根据CF:AF=BC:CF求出AF的长,进而可根据(2)的结果求出AD的长.
解答: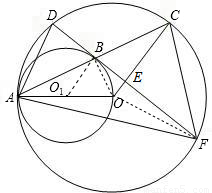 (1)证明:连接O1B,
(1)证明:连接O1B,
∵O1B=O1A,
∴∠O1AB=∠O1BA.
∵OA=OC,
∴∠OAC=∠OCA.
∴∠O1BA=∠OCA.
∴O1B∥OC.
∵OC⊥DF,
∴O1B⊥DF.
∴DF与⊙O1相切.
(2)证明:连接OB,则OB⊥AC,
∴AC=2AB=2BC.
∵OC⊥DF,
∴弧DC=弧CF.
∴∠CAD=∠CAF.
∵∠D=∠ACF,
∴△ABD∽△AFC.
∴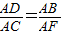 .
.
∵AC=2AB,
∴2AB2=AD•AF.
(3)解:直角△BEC中,BC=AB=2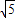 ,cos∠CBE=cos∠DBA=
,cos∠CBE=cos∠DBA=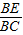 =
=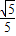 ,
,
∴BE=2,CE=4.
∵直角△OBE中,∠BOE=∠CBE=90°-∠BCO,BE=2,
∴BO=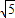 ,OE=1.
,OE=1.
∴AO=OC=OE+EC=5.
连接OF,直角△OEF中,OF=OA=5,OE=1,根据勾股定理有EF=2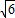 ,
,
∴BF=2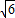 +2.
+2.
∵弧DC=弧CF,
∴∠CAF=∠BFC.
∴△ACF∽△FCB.
∴CF2=CB•CA=2AB2=40.
∴CF=2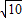 .
.
∴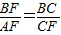 .
.
即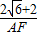 =
=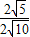 ,
,
∴AF=4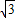 +2
+2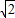 .
.
由(2)知:2AB2=AD•AF.
∴AD=4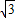 -2
-2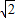 .
.
点评:本题主要考查了切线的判定、垂径定理、相似三角形的判定和性质等知识点,在(3)中通过相似三角形求出CF、AF的长是解题的关键.
(2)本题可通过证△ABD和△AFC相似来求解.连接OB,则OB⊥AC,因此可根据垂径定理得出AC=2AB,那么通过两三角形相似得出的AD:AC=AB:AF,即可得出所求的结论.
(3)本题可先求出BF的长,然后根据相似三角形FCB和ACF得出的CF 2=CB•CA,求出CF的长,还是这两个相似三角形,根据CF:AF=BC:CF求出AF的长,进而可根据(2)的结果求出AD的长.
解答:
 (1)证明:连接O1B,
(1)证明:连接O1B,∵O1B=O1A,
∴∠O1AB=∠O1BA.
∵OA=OC,
∴∠OAC=∠OCA.
∴∠O1BA=∠OCA.
∴O1B∥OC.
∵OC⊥DF,
∴O1B⊥DF.
∴DF与⊙O1相切.
(2)证明:连接OB,则OB⊥AC,
∴AC=2AB=2BC.
∵OC⊥DF,
∴弧DC=弧CF.
∴∠CAD=∠CAF.
∵∠D=∠ACF,
∴△ABD∽△AFC.
∴
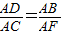 .
.∵AC=2AB,
∴2AB2=AD•AF.
(3)解:直角△BEC中,BC=AB=2
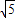 ,cos∠CBE=cos∠DBA=
,cos∠CBE=cos∠DBA=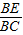 =
=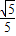 ,
,∴BE=2,CE=4.
∵直角△OBE中,∠BOE=∠CBE=90°-∠BCO,BE=2,
∴BO=
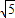 ,OE=1.
,OE=1.∴AO=OC=OE+EC=5.
连接OF,直角△OEF中,OF=OA=5,OE=1,根据勾股定理有EF=2
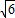 ,
,∴BF=2
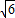 +2.
+2.∵弧DC=弧CF,
∴∠CAF=∠BFC.
∴△ACF∽△FCB.
∴CF2=CB•CA=2AB2=40.
∴CF=2
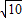 .
.∴
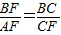 .
.即
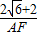 =
=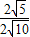 ,
,∴AF=4
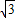 +2
+2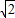 .
.由(2)知:2AB2=AD•AF.
∴AD=4
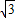 -2
-2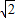 .
.点评:本题主要考查了切线的判定、垂径定理、相似三角形的判定和性质等知识点,在(3)中通过相似三角形求出CF、AF的长是解题的关键.

练习册系列答案
相关题目
 ;
;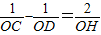 .
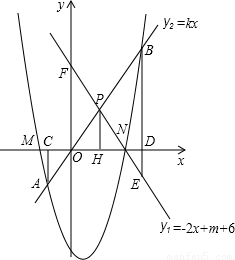
.
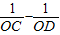 ;
;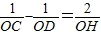 .
.
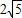 ,cos∠DBA=
,cos∠DBA=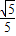 ,求AF和AD的长.
,求AF和AD的长.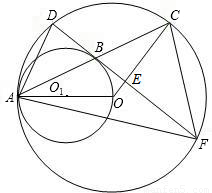
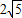 ,cos∠DBA=
,cos∠DBA=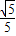 ,求AF和AD的长.
,求AF和AD的长.