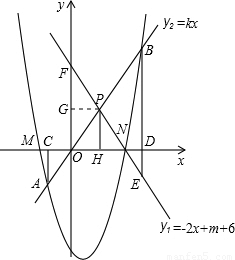
题目内容
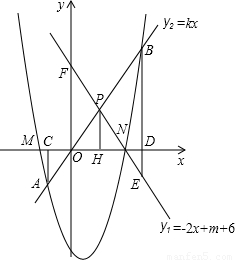
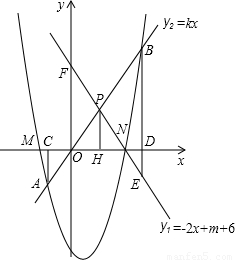
(2003•泰州)已知:如图,抛物线y=x2-(m+2)x+3(m-1)与x轴的两个交点M、N在原点的两侧,点N在点M的右边,直线y1=-2x+m+6经过点N,交y轴于点F.(1)求这条抛物线和直线的解析式.
(2)又直线y2=kx(k>0)与抛物线交于两个不同的点A、B,与直线y1交于点P,分别过点A、B、P作x轴的垂线,垂足分别是C、D、H.
①试用含有k的代数式表示
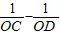 ;
;②求证:
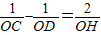 .
.(3)在(2)的条件下,延长线段BD交直线y1于点E,当直线y2绕点O旋转时,问是否存在满足条件的k值,使△PBE为等腰三角形?若存在,求出直线y2的解析式;若不存在,请说明理由.
【答案】分析:(1)可先根据直线y1的解析式求出N点的坐标,然后将其代入抛物线的解析式中即可求出m的值,然后根据M、N在原点两侧,即3(m-1)<0,将不合题意的m的值舍去,即可求出抛物线和直线的解析式;
(2)本题可联立个相交函数的解析式,求出C,D,H三点的横坐标,然后用根与系数的关系进行求解即可;
(3)本题要分三种情况进行讨论:
①当PB=BE时,则有∠OFD=∠OF,由于∠OFD为锐角且小于45°,因此∠FOB为钝角,此时直线y2的斜率k<0,显然不合题意.
②当PB=PE时,那么PF=PO,P点位于OF的垂直平分线上,因此P点的纵坐标为3,由此可求出P点的坐标.以此来求出直线y2的解析式.
③当PE=BE时,那么PF=OF=6,可过P作PG⊥y轴于G,通过构建相似三角形来求出P点的横坐标,进而根据直线y1的解析式求出P点的坐标,以此来求出直线y2的解析式.
综上所述,可求得符合条件的直线y2的解析式.
解答:解:(1)由题意可知:N点的坐标为(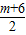 ,0).
,0).
已知抛物线过N点,则有:
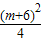 -
-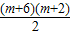 +3(m-1)+0
+3(m-1)+0
即m2-8m=0,解得m=0,m=8.
∵M,N在原点两侧,因此3(m-1)<0,m<1;
因此m=8不合题意舍去
∴m=0.
∴抛物线的解析式为y=x2-2x-3,直线的解析式为y1=-2x+6.
(2)已知抛物线与直线y2交于A、B两点,
因此kx=x2-2x+3,
即x2-(2+k)x-3=0
设C、D的坐标为(x1,0),(x2,0).
∴x1+x2=2+k,x1•x2=-3
∴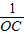 -
-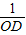 =
=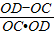 =
=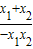 =
=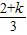 .
.
已知直线y2与y1交于P点,
则:-2x+6=kx,x=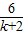
∴H点的坐标为(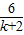 ,0)
,0)
因此 =
=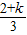 ,
,
∴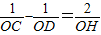 .
.
(3)本题要分三种情况:
①PB=BE,则有∠OFD=∠OPF,
∵∠OFD<45°,
∴∠FOB为钝角,此时y2的斜率k<0,
因此不合题意,不存在这种情况.
②PB=PE,则有PF=PO,设P点的坐标为(x,y),
∴y= OF=3.
OF=3.
已知直线y1过P点,
因此P点的坐标为( ,3).
,3).
∴3= k,k=2.
k,k=2.
因此直线y2的解析式为y2=2x.
③PE=BE,则有PF=OF=6.过P作PG⊥y轴于G,设点P的坐标为(x,y).
 在直角三角形OEF中,OE=3,OF=6,
在直角三角形OEF中,OE=3,OF=6,
根据勾股定理可得:EF=3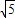 .
.
∵PG∥x轴
∴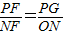 ,
,
即 .
.
∴x=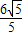 ,
,
由于直线y1=-2x+6过P点,
因此P点的坐标为(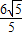 ,
,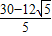 ).
).
∴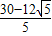 =k•
=k•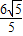 ,k=
,k= -2.
-2.
∴y2=(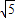 -2)x.
-2)x.
综上所述y2的解析式为y2=2x或y2=( -2)x.
-2)x.
点评:本题考查了一次函数和二次函数解析式的确定、二次函数与一元二次方程的关系、一元二次方程根与系数的关系、函数图象的交点、等腰三角形的构成情况等知识点,综合性强,主要考查学生分类讨论、数形结合的数学思想方法.
(2)本题可联立个相交函数的解析式,求出C,D,H三点的横坐标,然后用根与系数的关系进行求解即可;
(3)本题要分三种情况进行讨论:
①当PB=BE时,则有∠OFD=∠OF,由于∠OFD为锐角且小于45°,因此∠FOB为钝角,此时直线y2的斜率k<0,显然不合题意.
②当PB=PE时,那么PF=PO,P点位于OF的垂直平分线上,因此P点的纵坐标为3,由此可求出P点的坐标.以此来求出直线y2的解析式.
③当PE=BE时,那么PF=OF=6,可过P作PG⊥y轴于G,通过构建相似三角形来求出P点的横坐标,进而根据直线y1的解析式求出P点的坐标,以此来求出直线y2的解析式.
综上所述,可求得符合条件的直线y2的解析式.
解答:解:(1)由题意可知:N点的坐标为(
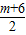 ,0).
,0).已知抛物线过N点,则有:
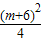 -
-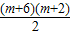 +3(m-1)+0
+3(m-1)+0即m2-8m=0,解得m=0,m=8.
∵M,N在原点两侧,因此3(m-1)<0,m<1;
因此m=8不合题意舍去
∴m=0.
∴抛物线的解析式为y=x2-2x-3,直线的解析式为y1=-2x+6.
(2)已知抛物线与直线y2交于A、B两点,
因此kx=x2-2x+3,
即x2-(2+k)x-3=0
设C、D的坐标为(x1,0),(x2,0).
∴x1+x2=2+k,x1•x2=-3
∴
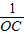 -
-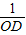 =
=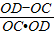 =
=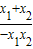 =
=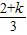 .
.已知直线y2与y1交于P点,
则:-2x+6=kx,x=
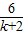
∴H点的坐标为(
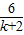 ,0)
,0)因此
 =
=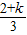 ,
,∴
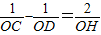 .
.(3)本题要分三种情况:
①PB=BE,则有∠OFD=∠OPF,
∵∠OFD<45°,
∴∠FOB为钝角,此时y2的斜率k<0,
因此不合题意,不存在这种情况.
②PB=PE,则有PF=PO,设P点的坐标为(x,y),
∴y=
 OF=3.
OF=3.已知直线y1过P点,
因此P点的坐标为(
 ,3).
,3).∴3=
 k,k=2.
k,k=2.因此直线y2的解析式为y2=2x.
③PE=BE,则有PF=OF=6.过P作PG⊥y轴于G,设点P的坐标为(x,y).
 在直角三角形OEF中,OE=3,OF=6,
在直角三角形OEF中,OE=3,OF=6,根据勾股定理可得:EF=3
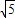 .
.∵PG∥x轴
∴
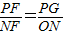 ,
,即
 .
.∴x=
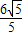 ,
,由于直线y1=-2x+6过P点,
因此P点的坐标为(
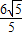 ,
,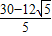 ).
).∴
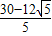 =k•
=k•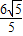 ,k=
,k= -2.
-2.∴y2=(
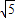 -2)x.
-2)x.综上所述y2的解析式为y2=2x或y2=(
 -2)x.
-2)x.点评:本题考查了一次函数和二次函数解析式的确定、二次函数与一元二次方程的关系、一元二次方程根与系数的关系、函数图象的交点、等腰三角形的构成情况等知识点,综合性强,主要考查学生分类讨论、数形结合的数学思想方法.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 ;
;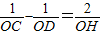 .
.
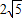 ,cos∠DBA=
,cos∠DBA=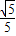 ,求AF和AD的长.
,求AF和AD的长.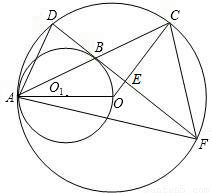
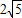 ,cos∠DBA=
,cos∠DBA=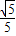 ,求AF和AD的长.
,求AF和AD的长.
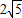 ,cos∠DBA=
,cos∠DBA=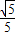 ,求AF和AD的长.
,求AF和AD的长.