题目内容
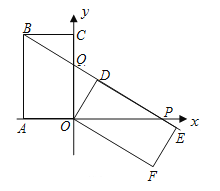
【题目】已知矩形OABC中，OA=3，AB=6，以OA、OC所在的直线为坐标轴，建立如图所示的平面直角坐标系。将矩形OABC绕点O顺时针方向旋转，得到矩形ODEF，当点B在直线DE上时，设直线DE和
轴交于点P，与
轴交于点Q．（1）求证：△BCQ≌△ODQ；（2）求点P的坐标；
【答案】（1）、证明过程见解析；（2）、（5,0）
【解析】试题分析：（1）、根据矩形的性质得出BC=OD，∠BCQ=∠ODQ=90°，结合∠BQC=∠OQD得出三角形全等；（2）、设CQ=x，则BQ=6－x，根据Rt△BCQ求出x的值，从而得出OQ的长度和点Q的坐标，求出直线BQ的解析式，根据解析式得出点P的坐标.
试题解析：（1）、∵矩形
和矩形
全等， ∴BC="OD," ∠BCQ=∠ODQ=90°，
∵∠BQC=∠OQD， ∴△BCQ≌△ODQ．
（2）、∵△BCQ≌△ODQ，∴CQ=DQ，BQ=OQ， 设CQ=x，则OQ=6-x，BQ=6-x，
在Rt△BCQ中，
， 解得
，
∴OQ=
，∴Q（0，
），
∵B（-3，6），设BQ:
，依题意得：
， 解得
，
∴
， 令
，得
， 解得
，∴P（5，0）.
练习册系列答案
相关题目
