题目内容
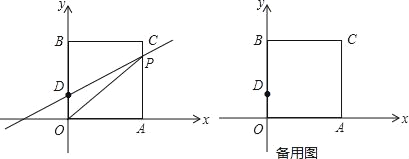
【题目】如图所示,已知抛物线经过点 A (-2,0)、 B (4,0)、 C (0,-8),抛物线 y = a x 2 + b x + c (a≠0)与直线 y = x -4交于 B , D 两点.

(1)求抛物线的解析式并直接写出 D 点的坐标;
(2)点 P 为抛物线上的一个动点,且在直线 BD 下方,试求出△ BDP 面积的最大值及此时点 P 的坐标;
(3)点 Q 是线段 BD 上异于 B 、 D 的动点,过点 Q 作 QF ⊥ x 轴于点 F , 交抛物线于点 G . 当△ QDG 为直角三角形时,求点 Q 的坐标.
【答案】(1) (-1,-5);(2) (![]() ,-
,-![]() );(3) (2,-2)或 (3,-1)
);(3) (2,-2)或 (3,-1)
【解析】试题分析:(1)设抛物线的解析式为y=a(x+2)(x-4),将点C的坐标代入可求得a的值,然后将y=x-4与抛物线的解析式联立求解即可;
(2)过点P作PE∥y轴,交直线AB与点E,设P(x,x2-2x-8),则E(x,x-4),则PE═-x2+3x+4,然后依据S△BDP=S△DPE+S△BPE,列出△BDP的面积与x的函数关系式,然后依据二次函数的性质求解即可;
(3)设直线y=x-4与y轴相交于点K,则K(0,-4),设G点坐标为(x,x2-2x-8),点Q点坐标为(x,x-4),先证明△QDG为等腰直角三角形,然后根据
∠QDG=90°和∠DGQ=90°两种情况求解即可.
试题解析:(1)设抛物线的解析式为y=a(x+2)(x-4),将点C的坐标代入得:-8a=-8,解得:a=1,
∴抛物线的解析式为y=x2-2x-8.
将y=x-4代入抛物线的解析式得:x2-2x-8=x-4,解得:x=4或x=-1,
将x=-1代入y=x-4得:y=-5.
∴D(-1,-5).
(2)如图所示:
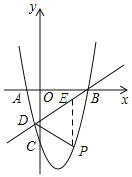
过点P作PE∥y轴,交直线AB与点E,设P(x,x2-2x-8),则E(x,x-4).
∴PE=x-4-(x2-2x-8)=-x2+3x+4.
∴S△BDP=S△DPE+S△BPE=![]() PE(xp-xD)+
PE(xp-xD)+![]() PE(xB-xE)=
PE(xB-xE)=![]() PE(xB-xD)=
PE(xB-xD)=![]() (-x2+3x+4)=-
(-x2+3x+4)=-![]() (x-
(x-![]() )2+
)2+![]() .
.
∴当x=![]() 时,△BDP的面积的最大值为
时,△BDP的面积的最大值为![]() .
.
∴P(![]() ,-
,-![]() ).
).
(3)设直线y=x-4与y轴相交于点K,则K(0,-4),设G点坐标为(x,x2-2x-8),点Q点坐标为(x,x-4).
∵B(4,0),
∴OB=OK=4.
∴∠OKB=∠OBK=45°.
∵QF⊥x轴,
∴∠DQG=45°.
若△QDG为直角三角形,则△QDG是等腰直角三角形.
①当∠QDG=90°时,过点D作
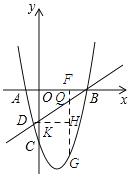
∴QG=2DH,QG=-x2+3x+4,DH=x+1,
∴-x2+3x+4=2(x+1),解得:x=-1(舍去)或x=2,
∴Q1(2,-2).
②当∠DGQ=90°,则DH=QH.
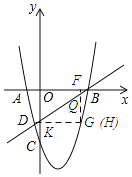
∴-x2+3x+4=x+1,解得x=-1(舍去)或x=3,
∴Q2(3,-1).
综上所述,当△QDG为直角三角形时,点Q的坐标为(2,-2)或(3,-1).