题目内容
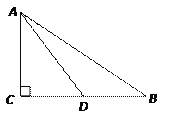
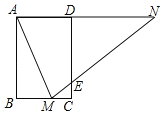
【题目】如图,矩形ABCD中,AB=3,BC=2,点M在BC上,连接AM,作∠AMN=∠AMB,点N在直线AD上,MN交CD于点E.
(1)求证:△AMN是等腰三角形;
(2)求证:AM2=2BMAN;
(3)当M为BC中点时,求ME的长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)利用矩形和平行线的性质求证∠AMN=∠NAM,从而等角对等边;(2)根据等腰三角形和相似三角形的性质列比例式,得到ANBM=AHAM=![]() AM2,从而求证;(3)由(2)的结论和已知条件求得AN=5,DN=3,然后根据平行线判定△DNE∽△CME,从而列出比例式求DE的长度,最后利用勾股定理求解.
AM2,从而求证;(3)由(2)的结论和已知条件求得AN=5,DN=3,然后根据平行线判定△DNE∽△CME,从而列出比例式求DE的长度,最后利用勾股定理求解.
(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠NAM=∠BMA,
∵∠AMN=∠AMB,
∴∠AMN=∠NAM,
∴AN=MN,即△AMN是等腰三角形;
(2)∵四边形ABCD是矩形,
∴AD∥BC,AD=BC=2,AB=CD=3,
∴∠NAM=∠BMA,
作NH⊥AM于H,如图所示:
∵AN=MN,NH⊥AM,
∴AH=![]() AM,
AM,
∵∠NHA=∠ABM=90°,∠NAM=∠BMA,
∴△NAH∽△AMB,
∴![]() ,
,
∴ANBM=AHAM=![]() AM2,
AM2,
∴AM2=2BMAN;

(3)∵M为BC中点,
∴BM=CM=![]() BC=
BC=![]() ×2=1,
×2=1,
由(2)得:AM2=2BMAN,
即:AM2=2AN,
∵AM2=AB2+BM2=32+12=10,
∴10=2AN,
∴AN=5,
∴DN=AN﹣AD=5﹣2=3,
设DE=x,则CE=3﹣x,
∵AN∥BC,
∴△DNE∽△CME
∴![]() ,即
,即![]() ,
,
解得:x=![]() ,即DE=
,即DE=![]() ,
,
∴CE=DC﹣DE=3﹣![]() =
=![]() ,
,
∴在Rt△MEC中,ME=![]() .
.

【题目】为迎接“世界华人炎帝故里寻根节”,某工厂接到一批纪念品生产订单,按要求在15天内完成,约定这批纪念品的出厂价为每件20元,设第x天(1≤x≤15,且x为整数)每件产品的成本是p元,p与x之间符合一次函数关系,部分数据如表:
天数(x) | 1 | 3 | 6 | 10 |
每件成本p(元) | 7.5 | 8.5 | 10 | 12 |
任务完成后,统计发现工人李师傅第x天生产的产品件数y(件)与x(天)满足如下关系:y=![]() ,
,
设李师傅第x天创造的产品利润为W元.
(1)直接写出p与x,W与x之间的函数关系式,并注明自变量x的取值范围:
(2)求李师傅第几天创造的利润最大?最大利润是多少元?
(3)任务完成后.统计发现平均每个工人每天创造的利润为299元.工厂制定如下奖励制度:如果一个工人某天创造的利润超过该平均值,则该工人当天可获得20元奖金.请计算李师傅共可获得多少元奖金?