题目内容
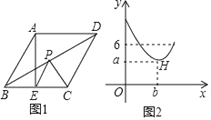
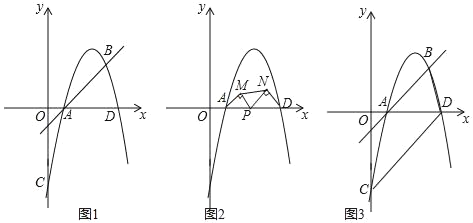
【题目】如图1,在平面直角坐标系中,直线y=x﹣1与抛物线y=﹣x2+bx+c交于A、B两点,其中A(m,0)、B(4,n),该抛物线与y轴交于点C,与x轴交于另一点D.
(1)求m、n的值及该抛物线的解析式;
(2)如图2,若点P为线段AD上的一动点(不与A、D重合),分别以AP、DP为斜边,在直线AD的同侧作等腰直角△APM和等腰直角△DPN,连接MN,试确定△MPN面积最大时P点的坐标;
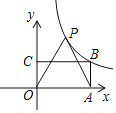
(3)如图3,连接BD、CD,在线段CD上是否存在点Q,使得以A、D、Q为顶点的三角形与△ABD相似,若存在,请直接写出点Q的坐标;若不存在,请说明理由.
【答案】(1)m=1,n=3, y=﹣x2+6x﹣5;(2) 当m=2,即AP=2时,S△MPN最大,此时OP=3,即P(3,0);(3)存在,点Q的坐标为(2,﹣3)或(![]() ),理由见解析
),理由见解析
【解析】
(1)把A与B坐标代入一次函数解析式求出m与n的值,确定出A与B坐标,代入二次函数解析式求出b与c的值即可;
(2)由等腰直角△APM和等腰直角△DPN,得到∠MPN为直角,由两直角边乘积的一半表示出三角形MPN面积,利用二次函数性质确定出三角形面积最大时P的坐标即可;
(3)存在,分两种情况,根据相似得比例,求出AQ的长,利用两点间的距离公式求出Q坐标即可.
解:(1)把A(m,0),B(4,n)代入y=x﹣1得:m=1,n=3,
∴A(1,0),B(4,3),
∵y=﹣x2+bx+c经过点A与点B,
∴![]() ,
,
解得:![]() ,
,
则二次函数解析式为y=﹣x2+6x﹣5;
(2)如图2,△APM与△DPN都为等腰直角三角形,
∴∠APM=∠DPN=45°,
∴∠MPN=90°,
∴△MPN为直角三角形,
令﹣x2+6x﹣5=0,得到x=1或x=5,
∴D(5,0),即DA=5﹣1=4,
设AP=m,则有DP=4﹣m,
∴PM=![]() m,PN=
m,PN=![]() (4﹣m),
(4﹣m),
∴S△MPN=![]() PMPN=
PMPN=![]() ×
×![]() m×
m×![]() (4﹣m)=﹣
(4﹣m)=﹣![]() m2+m=﹣
m2+m=﹣![]() (m﹣2)2+1,
(m﹣2)2+1,
∴当m=2,即AP=2时,S△MPN最大,此时OP=3,即P(3,0);
(3)存在,
易得直线CD解析式为y=x﹣5,设Q(x,x﹣5),
由题意得:∠BAD=∠ADC=45°,
当△ABD∽△/span>DAQ时,![]() ,即
,即![]() ,
,
解得:AQ=![]() ,
,
由两点间的距离公式得:(x﹣1)2+(x﹣5)2=![]() ,
,
解得:x=![]() 或x=
或x=![]() ,此时Q(
,此时Q(![]() ,﹣
,﹣![]() )或(
)或(![]() ,﹣
,﹣![]() )(舍去);
)(舍去);
当△ABD∽△DQA时,![]() =1,即AQ=
=1,即AQ=![]() ,
,
∴(x﹣1)2+(x﹣5)2=10,
解得:x=2或x=4,此时Q(2,﹣3)或(4,﹣1)(舍去),
综上,点Q的坐标为(2,﹣3)或(![]() ).
).

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
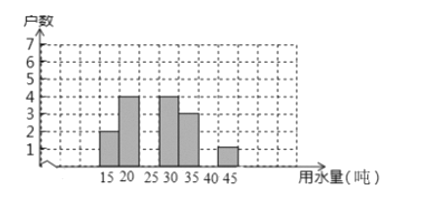
一线名师权威作业本系列答案【题目】下表是2019年三月份某居民小区随机抽取20户居民的用水情况:
用水量/吨 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
户数 | 2 | 4 | m | 4 | 3 | 0 | 1 |
(1)求出m= ,补充画出这20户家庭三月份用电量的条形统计图;
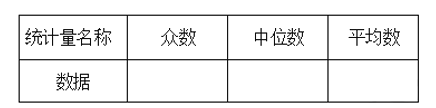
(2)据上表中有关信息,计算或找出下表中的统计量,并将结果填入表中:
(3)为了倡导“节约用水,绿色环保”的意识,台州市自来水公司实行“梯级用水、分类计费”,价格表如下:

如果该小区有500户家庭,根据以上数据,请估算该小区三月份有多少户家庭在ⅠI级标准?并估算这些级用水户的总水费是多少?