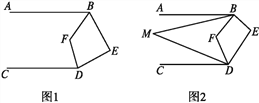
题目内容
【题目】如图，在ABDC中，分别取AC、BD的中点E和F，连接BE、CF，过点A作AP∥BC，交DC的延长线于点P． 
（1）求证：△ABE≌△DCF；
（2）当∠P满足什么条件时，四边形BECF是菱形？证明你的结论．
【答案】
（1）证明：在ABDC中，∠BAC=∠D，AB=CD，AC=BD，
∵E、F分别是AC、BD的中点，
∴AE=DF，
在△ABE和△DCF中， 
，
∴△ABE≌△DCF（SAS）；
（2）解：∠P=90°时，四边形BECF是菱形．理由如下：
在ABCD中，AB∥CD，
∵AP∥BC，
∴四边形ABCP是平行四边形，
∴∠ABC=∠P=90°，
∵E是AC的中点，
∴BE=CE= 
AC，
∵E、F分别是AC、BD的中点，
∴BF=CE，
又∵AC∥BD，
∴四边形BECF是平行四边形，
∴四边形BECF是菱形（邻边相等的平行四边形是菱形）．
【解析】（1）根据平行四边形的对角相等可得∠BAC=∠D，对边相等可得AB=CD，AC=BD，再根据中点定义求出AE=DF，然后利用“边角边”证明即可；（2）∠P=90°时，四边形BECF是菱形．先判断出四边形ABCP是平行四边形，根据平行四边形的对角相等可得∠ABC=∠P，再根据直角三角形斜边上的中线等于斜边的一半可得BE=CE，利用一组对边平行且相等的四边形是平行四边形判断出四边形BECF是平行四边形，然后根据邻边相等的平行四边形是菱形证明．
【考点精析】本题主要考查了平行四边形的性质和菱形的判定方法的相关知识点，需要掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分；任意一个四边形，四边相等成菱形；四边形的对角线，垂直互分是菱形．已知平行四边形，邻边相等叫菱形；两对角线若垂直，顺理成章为菱形才能正确解答此题．
