题目内容
 已知,如图,D(0,1),⊙D交y轴于A、B两点,交x轴负半轴于C点,过C点的直线:y=-2x-4与y轴交于P.
已知,如图,D(0,1),⊙D交y轴于A、B两点,交x轴负半轴于C点,过C点的直线:y=-2x-4与y轴交于P.
(1)试猜想PC与⊙D的位置关系,并说明理由.
(2)判断在直线PC上是否存在点E,使得S△EOC=4S△CDO?若存在,求出点E的坐标;若不存在,请说明理由.
解:(1)PC与⊙D的位置关系是相切.理由如下:
在y=-2x-4中,得C(-2,0),P(0,-4),
则CD2=4+1=5,CP2=4+16=20,PD2=(1+4)2=25,
则CD2+CP2=PD2,
∴∠DCP=90°,
∴PC与⊙D的位置关系是相切.
(2)∵S△CDO=1,
∴S△EOC=4S△CDO=4,
又OC=2,
∴点E到OC的距离是4,即点E的纵坐标是±4.
当y=4时,则x=4;当y=-4时,则x=0.
即E(-4,4)或(0,-4).
分析:(1)分别求得点C、P的坐标,再根据勾股定理的逆定理得到直角三角形,从而根据切线的判定即可证明;
(2)首先求得三角形COD的面积,进而求得三角形EOC的面积,根据OC的长,确定点E的纵坐标,再根据直线的解析式求得点E的横坐标即可.
点评:此题综合考查了直线和坐标轴的交点求法、勾股定理的逆定理、切线的判定以及三角形的面积公式.
在y=-2x-4中,得C(-2,0),P(0,-4),
则CD2=4+1=5,CP2=4+16=20,PD2=(1+4)2=25,
则CD2+CP2=PD2,
∴∠DCP=90°,
∴PC与⊙D的位置关系是相切.
(2)∵S△CDO=1,
∴S△EOC=4S△CDO=4,
又OC=2,
∴点E到OC的距离是4,即点E的纵坐标是±4.
当y=4时,则x=4;当y=-4时,则x=0.
即E(-4,4)或(0,-4).
分析:(1)分别求得点C、P的坐标,再根据勾股定理的逆定理得到直角三角形,从而根据切线的判定即可证明;
(2)首先求得三角形COD的面积,进而求得三角形EOC的面积,根据OC的长,确定点E的纵坐标,再根据直线的解析式求得点E的横坐标即可.
点评:此题综合考查了直线和坐标轴的交点求法、勾股定理的逆定理、切线的判定以及三角形的面积公式.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
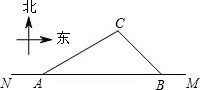 ,测得C在B的北偏西45°方向上.
,测得C在B的北偏西45°方向上.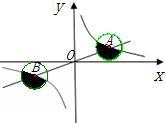 11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为
11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为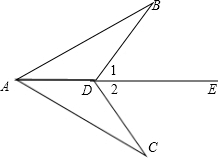 已知,如图,∠1=∠2,
已知,如图,∠1=∠2,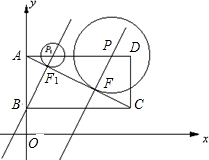 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为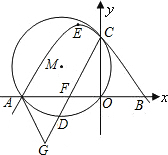 于C点,⊙M经过原点O及点A、C,点D是劣弧
于C点,⊙M经过原点O及点A、C,点D是劣弧