题目内容
(2009•卢湾区二模)在等腰△ABC中,已知AB=AC=3, ,D为AB上一点,过点D作DE⊥AB交BC边于点E,过点E作EF⊥BC交AC边于点F.
,D为AB上一点,过点D作DE⊥AB交BC边于点E,过点E作EF⊥BC交AC边于点F.(1)当BD长为何值时,以点F为圆心,线段FA为半径的圆与BC边相切;
(2)过点F作FP⊥AC,与线段DE交于点G,设BD长为x,△EFG的面积为y,求y关于x的函数解析式及其定义域.

【答案】分析:(1)过点A作AM⊥BC,垂足为点M,根据已知可求得BC的长,再根据三角函数即可求得BD的长.
(2)根据已知可得到△ABC∽△EFG,根据相似三角形的面积比等于相似比的平方即可求得函数解析式.
解答: 解:(1)过点A作AM⊥BC,垂足为点M,
解:(1)过点A作AM⊥BC,垂足为点M,
在Rt△ABM中,cos∠B= ,AB=3,
,AB=3,
∴BM=1.
∵AB=AC,AM⊥BC,
∴BC=2.
设BD长为x,
在Rt△BDE中,cos∠B= ,
,
∴BE=3x,EC=2-3x.
同理FC=6-9x,FE=4 -6
-6 x.
x.
∴AF=9x-3.
由题意得9x-3=4 -6
-6 x.
x.
解得x=2 -
- .
.
(2)∵DE⊥AB,EF⊥BC,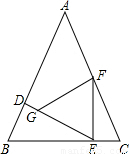
∴∠B+∠BED=90°,∠DEF+∠BED=90°.
∴∠B=∠DEF.
同理∠EFG=∠C.
∴△ABC∽△EFG.
∴ =(
=( )2
)2
∴ =(
=( )2
)2
∴y=36 x2-48
x2-48 x+16
x+16 .
.
∵△ABC∽△EFG,
∴BC:EF=AB:GE,
∴2:(4 -6
-6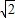 x)=3:GE,
x)=3:GE,
∴GE=6 -9
-9 x.
x.
∵在△BDE中,∠BDE=90°,BD=x,BE=3x,
∴DE=2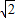 x.
x.
∴DG=DE-GE=2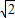 x-(6
x-(6 -9
-9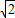 x)=11
x)=11 x-6
x-6 .
.
∵点G在线段DE上,EG为△EFG的一条边,
∴DG≥0,且EG>0,
∴11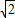 x-6
x-6 ≥0,且6
≥0,且6 -9
-9 x>0,
x>0,
解得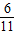 ≤x<
≤x< .
.
点评:本题主要考查了等腰三角形的性质,相似三角形的性质以及解直角三角形的应用等知识点,弄清各边之间的关系是解题的关键.
(2)根据已知可得到△ABC∽△EFG,根据相似三角形的面积比等于相似比的平方即可求得函数解析式.
解答:
 解:(1)过点A作AM⊥BC,垂足为点M,
解:(1)过点A作AM⊥BC,垂足为点M,在Rt△ABM中,cos∠B=
 ,AB=3,
,AB=3,∴BM=1.
∵AB=AC,AM⊥BC,
∴BC=2.
设BD长为x,
在Rt△BDE中,cos∠B=
 ,
,∴BE=3x,EC=2-3x.
同理FC=6-9x,FE=4
 -6
-6 x.
x.∴AF=9x-3.
由题意得9x-3=4
 -6
-6 x.
x.解得x=2
 -
- .
.(2)∵DE⊥AB,EF⊥BC,

∴∠B+∠BED=90°,∠DEF+∠BED=90°.
∴∠B=∠DEF.
同理∠EFG=∠C.
∴△ABC∽△EFG.
∴
 =(
=( )2
)2∴
 =(
=( )2
)2∴y=36
 x2-48
x2-48 x+16
x+16 .
.∵△ABC∽△EFG,
∴BC:EF=AB:GE,
∴2:(4
 -6
-6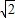 x)=3:GE,
x)=3:GE,∴GE=6
 -9
-9 x.
x.∵在△BDE中,∠BDE=90°,BD=x,BE=3x,
∴DE=2
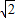 x.
x.∴DG=DE-GE=2
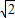 x-(6
x-(6 -9
-9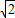 x)=11
x)=11 x-6
x-6 .
.∵点G在线段DE上,EG为△EFG的一条边,
∴DG≥0,且EG>0,
∴11
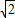 x-6
x-6 ≥0,且6
≥0,且6 -9
-9 x>0,
x>0,解得
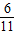 ≤x<
≤x< .
.点评:本题主要考查了等腰三角形的性质,相似三角形的性质以及解直角三角形的应用等知识点,弄清各边之间的关系是解题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目

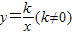 经过点(2,-3),那么k= .
经过点(2,-3),那么k= .